随机森林 2（决策树）

通过 随机森林 1 的介绍，相信大家对随进森林都有了一个初步的认知，知道了随机和森林分别指的是什么，以及决策树根据什么选择内部节点。本文将会从森林深入到树，去看一下决策树是如何构建的。网上很多文章都讲了决策树如何构建，但在我看来不够生动形象，不够深入，希望此文能够让你彻彻底底了解决策树以及公式的含义。

一、决策树的核心与逻辑

决策树的核心是确定节点用哪个特征当做判断条件，优先选择分类效果最强的特征当做节点的判断条件。构建决策树的逻辑也就清晰了，根节点选择分类效果最强的特征当做判断标准，后面的节点依次选择剩余特征种分类最强的特征当做判断标准，如果两个一样强，那就形成分支，最终构建成一棵树。

二、衡量特征分类效果强弱的指标

随进森林和决策树构建的逻辑我们已经非常清楚了，我们只要知道如何判断判断特征分类效果的强弱就可以一通百顺。这里我们会讲四个指标，分别是信息熵、信息增益、信息增益率和基尼指数。

2.1 信息熵

熵大家应该都听说过，熵是用来衡量混乱程度的指标，越有序，熵越小，也可以理解为纯度的指标，越纯，熵越小。

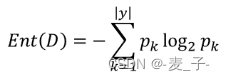
Ent(D)表示样本集合 D 的信息熵；表示 k 类样本所占的比例；所以信息熵就是计算每个类别的累加；

因为0<<1，所以越接近 1， 也就是 k 的概率接近 1，越接近 0，熵越小；相反 k 的概率越小，熵越大。举个极端的例子：假如只有一个类别，那么这个类别的概率肯定是 1，非常纯，非常有序，熵也达到了最小值 0。

这里延伸一下为什么很多公式都带 log，本质是为了让差值小的两个数字经过 log 计算后，让差值更明显。在这里因为概率之间的差异非常小，可能差异在 0.1 甚至 0.01，计算以 2 为底的，0.01 和 0.02 的对数，?结果分别时-6.644和-5.644，差异增加了 100 倍。

2.2 信息增益

我们知道了熵可以描述一个集合的纯度，那么如何利用熵来决定节点选择哪个特征划分呢？这里就引入了信息增益的概念，信息增益表示的是熵减少的程度。划分逻辑就是，划分后多个集合熵的和与划分前熵相比较，减少的多说明划分效果好。

举个例子，集合 A 为[1,1,1,2,2,2]，经过特征 X 划分为 集合 B1[1,1,2,2] 和集合 B2[1,2]，经过特征 Y?划分为集合 C1[1,1,1] 和集合 C2[2,2,2]。我们先计算下 A 的熵==-1，然后计算下划分后的熵，B1 的熵=B2 的熵==-1， B1 的熵和 B2 的熵相加等于 -2；C1 的熵=C2 的熵= 0，C1 和 C2 的熵相加等于 0。通过特征 X 划分，熵从-1 变成-2，通过特征 Y 的划分，熵从-1 变成 0，很明显特征 Y 划分效果好，所以选择 Y 当做该节点划分特征。

2.3 信息增益率

2.4 基尼指数