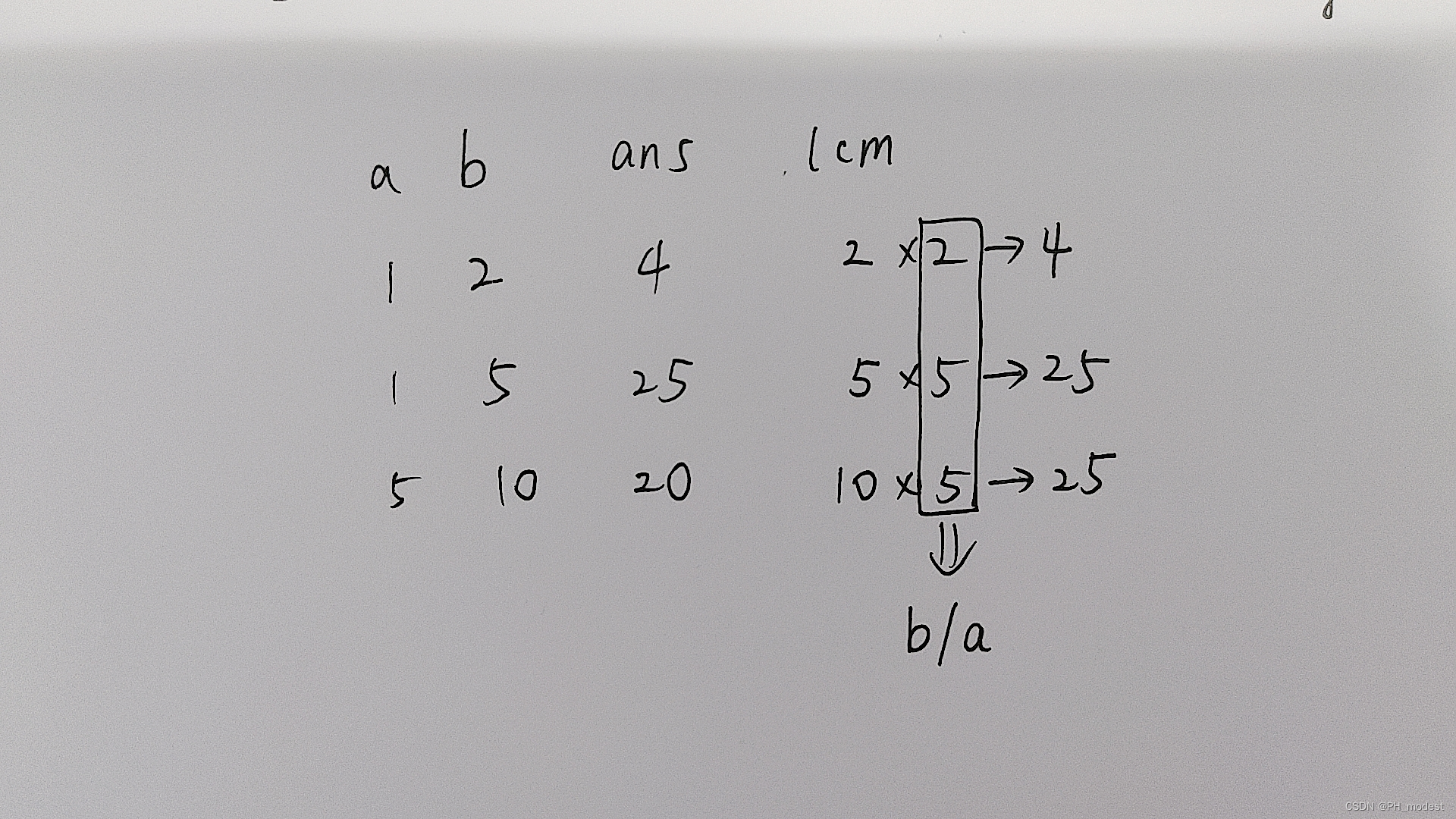【CF比赛记录】—— Good Bye 2023(A、B、C)
🌏博客主页:PH_modest的博客主页
🚩当前专栏:CF比赛记录
💌其他专栏:
🔴每日一题
🟡 cf闯关练习
🟢 C语言跬步积累
🌈座右铭:广积粮,缓称王!
A. 2023
👉传送门👈

题目大意:
在一个乘积等于
2023
2023
2023 的序列
a
a
a 中,去掉了
k
k
k 个数字,剩下一个长度为
n
n
n 的序列
b
b
b 。给定所得到的序列
b
b
b ,找出任何合适的序列
a
a
a 并输出从中删除了哪些
k
k
k 元素,或者指出这样的序列不可能存在。
请注意,我们并不保证存在这样的序列。
1.Tutorial
2023的因子只有1、7、17、119、289 、2023,先求出给出元素之积,然后判断这个数是不是2023的因子,如果是就直接输出2023除以这个数的值,剩下的数直接输出1.
2.Solution(赛时写的屎山代码,将就着看吧)
//https://codeforces.com/contest/1916/problem/A
//
//
#include<iostream>
#include<algorithm>
#include<string>
#include<deque>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<cstring>
#define int long long
using namespace std;
int s[200020];
void solve()
{
int n,k;
cin>>n>>k;
int cj=1;
int ans=2023;
for(int i=0;i<n;i++)
{
cin>>s[i];
cj*=s[i];
}
if(cj==1||cj==7||cj==17||cj==119||cj==289||cj==2023)
{
cout<<"YES"<<"\n";
if(cj==1)
{
cout<<"2023 ";
for(int i=0;i<k-1;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
if(cj==7)
{
cout<<"289 ";
for(int i=0;i<k-1;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
if(cj==17)
{
cout<<"119 ";
for(int i=0;i<k-1;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
if(cj==119)
{
cout<<"17 ";
for(int i=0;i<k-1;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
if(cj==289)
{
cout<<"7 ";
for(int i=0;i<k-1;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
if(cj==2023)
{
for(int i=0;i<k;i++)
{
cout<<"1 ";
}
cout<<"\n";
return;
}
}
else
{
cout<<"NO"<<"\n";
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
B. Two Divisors
👉传送门👈

题目大意:
选择某个数字 1 ≤ x ≤ 1 0 9 1 \le x \le 10^9 1≤x≤109 。给你两个整数 a a a 和 b b b ,它们是数 x x x 的两个最大除数。同时满足条件1 ≤ a < b < x 。
对于给定的数 a a a , b b b , 你需要求出 x x x 的值。
? ^{\dagger} ? 如果有整数 k k k 使得 x = y ? k x = y \cdot k x=y?k 是整数 x x x 的整除,那么数 y y y 是整数 x x x 的整除。
1.Tutorial
求最小公倍数再考虑这个最小公倍数是否等于b,如果等于就用b/a*这个最小公倍数
- 首先看到题目肯定先想到求a,b的最小公倍数,这样求完的结果不是最终的答案,当b是a的倍数时,最小公倍数是b但是题目中表示b < x的,所以还需要考虑当b是a的倍数时该怎么办
- 由图可知当所求的最小公倍数等于b的时候,就用最小公倍数*b/a
2.Solution
//https://codeforces.com/contest/1916/problem/B
//求最小公倍数再考虑这个最小公倍数是否等于b,如果等于就用b/a*这个最小公倍数
//
#include<iostream>
#include<algorithm>
#include<string>
#include<deque>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<cstring>
#define int long long
using namespace std;
void solve()
{
int a,b;
cin>>a>>b;
int c=a/__gcd(a,b)*b;
if(c==b)
{
cout<<b/a*c<<"\n";
}
else
{
cout<<c<<"\n";
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
3.Conclusion
C. Training Before the Olympiad
👉传送门👈

1.Tutorial
- 考虑奇数的个数,假设个数为x,有一个x/3,结果就需要-1,在判断x%3是否等于1,如果等于就还需要再减一
- 这里需要知道奇数和偶数进行那个操作时结果会 -1,题目的意思就是让这个操作尽可能的
2.Solution
//https://codeforces.com/contest/1916/problem/C
//考虑奇数的个数,假设个数为x,有一个x/3,结果就需要-1,在判断x%3是否等于1,如果等于就还需要再减一
//
#include<iostream>
#include<algorithm>
#include<string>
#include<deque>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<cstring>
#define int long long
using namespace std;
int s[200020];
int odd[200020];//奇数的个数
void solve()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>s[i];
}
if(s[0]%2==1)
{
odd[0]=1;
}
else
{
odd[0]=0;
}
for(int i=1;i<n;i++)//求前i个数有多少个奇数
{
if(s[i]%2==1)
{
odd[i]=odd[i-1]+1;
}
else
{
odd[i]=odd[i-1];
}
}
int sum=0;
for(int i=0;i<n;i++)
{
sum+=s[i];
if(i==0)
{
cout<<sum<<" ";
continue;
}
int x=odd[i]%3;
int y=odd[i]/3;
if(x==1)
{
cout<<sum-y-1<<" ";
}
else
{
cout<<sum-y<<" ";
}
}
cout<<"\n";
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
3.Conclusion
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!