【网络安全】网络防护之旅 - 非对称密钥体制的解密挑战

2023-12-16 09:45:53

🌈个人主页：Sarapines Programmer
🔥?系列专栏：《网络安全之道 | 数字征程》
?墨香寄清辞：千里传信如电光，密码奥妙似仙方。 挑战黑暗剑拔弩张，网络战场誓守长。

目录

😈1. 初识网络安全

😈2.?非对称密钥体制的解密挑战

🕵??♂?2.1 研究目的

🕵??♂?2.2 研究环境

🕵??♂?2.3 研究要求

🕵??♂?2.4 研究内容

🛰?2.4.1 非对称加密体制

🛰?2.4.2 RES加密技术

🛰?2.4.3 研究结果

🕵??♂?2.5 研究记录

📝总结

😈1. 初识网络安全

网络安全的基本认识

网络安全是一门关注计算机系统和网络安全的专业学科。其首要任务是维护信息系统的核心价值，包括机密性、完整性和可用性，以对抗未经授权的访问、破坏、篡改或泄露的威胁。

核心职责：

  1. 访问控制与身份认证： 制定并实施强有力的访问控制策略，以确保只有授权用户能够获取敏感信息。

  2. 加密技术： 运用复杂的加密算法，保障数据在传输和存储中的安全性，从而抵御窃听和篡改的风险。

  3. 安全基础设施： 部署防火墙、入侵检测与防御系统等，构筑坚实的安全基础设施，为网络提供全方位的保护。

高级技术手段：

  1. 漏洞扫描与修复： 采用主动扫描技术，及时发现系统漏洞和弱点，迅速修复以预防可能的攻击。

  2. 恶意软件检测与清除： 运用先进的恶意软件检测技术，及时清除潜在威胁，确保系统的持续安全。

  3. 网络流量分析： 通过深度分析网络流量，察觉异常行为，提前识别潜在风险，从而及时采取防范措施。

挑战与创新：

随着信息技术的不断进步，网络安全面临着日益复杂和多样化的威胁。科研者通过持续创新，深入研究各种安全技术，努力构建更加健壮、智能的网络安全体系，以确保数字空间中的数据和系统能够在一个安全、稳定的环境中运行。

😈2.?非对称密钥体制的解密挑战

🕵??♂?2.1 研究目的

  1. 深度解析非对称加密机制：这次实验旨在通过深入研究RSA算法，全面理解非对称加密的核心原理。通过实际操作密钥生成、加密和解密，深入挖掘非对称加密在保护通信和数据传输中的至关重要作用，培养对加密算法实际运用的深刻认知。
  2. 精通RSA算法的操作步骤：透过实际操练，掌握生成RSA密钥对、加密和解密数据的步骤。深入了解非对称加密体系的详尽操作流程，包括密钥生成、加密和解密的关键步骤，为后续安全通信的实际应用奠定坚实基础。
  3. 深入了解数字签名的应用：这次实验的目标在于介绍数字签名的实际应用。通过使用私钥对消息进行签名，理解数字签名在验证信息完整性方面的关键作用。透过验证签名的过程，培养对数字签名技术在数据传输中实际应用的深刻认知。
  4. 掌握密钥交换的原理与应用技巧：学习RSA算法在密钥交换中的实际运用，透过实际操作了解如何使用对方的公钥进行安全的对称密钥交换。精通密钥交换的原理，培养在实际通信中选择安全密钥交换方式的能力。

🕵??♂?2.2 研究环境

  1. Java编程环境配置：

    在进行深度研究时，我们选择了Visual Studio Code（VSCode）作为主要Java编程环境。这包括对Java编程语言及其相关库，如Java Standard Edition (Java SE)，的全面支持。作为集成开发环境（IDE），我们可选用Eclipse或IntelliJ IDEA，确保配置完善的Java Development Kit（JDK）。

  2. 网络安全实验库和工具的选择：

    在进行网络安全实验时，我们精心挑选了一系列库和工具，以确保研究的深度和广度。这些包括但不限于：

    • Apache Commons Codec，用于进行高效的加密和解密操作。
    • Java Cryptography Architecture（JCA），提供对安全算法的高效实现。
    • Java Cryptography Extension（JCE），扩展Java的加密功能，提供更多的加密算法选择。
    • Wireshark，作为网络流量分析和协议分解的强大工具。
    • JUnit，用于编写和执行网络安全测试用例，确保实验的可靠性和稳定性。

  3. 硬件环境要求：

    我们要求在进行网络安全实验时，使用具备强大计算资源的硬件环境。这包括足够的内存和高性能的CPU/GPU，以确保实验的效率和准确性。

    同时，我们强调确保网络连接的稳定性，这是进行网络安全漏洞测试和分析的基础。只有在网络连接稳定的环境下，我们才能全面深入地探讨和解决网络安全领域的挑战。

🕵??♂?2.3 研究要求

  1. 背景介绍 在信息安全领域中，非对称加密是一种重要的加密体制，与对称加密不同，非对称加密使用一对密钥，即公钥和私钥，以确保安全的数据传输和存储。

  2. 非对称加密的基本原理

    • 密钥对： 包括公钥和私钥，公钥用于加密，私钥用于解密。
    • 加密过程： 发送者使用接收者的公钥对消息进行加密。
    • 解密过程： 接收者使用自己的私钥对加密消息进行解密。

  3. RSA算法

    • 算法简介： RSA是一种常用的非对称加密算法，基于大整数的因子分解难题。
    • 密钥生成： 包括生成两个大素数、计算模数和公私钥指数。
    • 加密过程： 使用接收者的公钥对明文进行加密。
    • 解密过程： 接收者使用自己的私钥对密文进行解密。

  4. 运行RSA算法实现对字符串的加解密

    • 实验环境搭建： 在合适的开发环境中配置RSA算法所需的库和工具。
    • 字符串加密： 利用RSA算法对给定字符串进行加密，确保仅有拥有私钥的一方能够解密。
    • 字符串解密： 使用相应的私钥对加密后的字符串进行解密，还原原始明文。

  5. 实验效果与应用场景

    • 验证正确性： 确保加解密的过程符合RSA算法的规范。
    • 应用场景： 探讨RSA算法在实际场景中的应用，如安全通信、数字签名等。

通过深入研究非对称加密体制的基本原理和实际运行RSA算法对字符串进行加解密，我们能够更全面地理解非对称加密的机制，为信息安全领域的高级应用奠定坚实的基础。

🕵??♂?2.4 研究内容

🛰?2.4.1 非对称加密体制

非对称加密体制，亦被冠以公钥加密体制之名，为密码学领域的精妙原理，与对称加密方式有着根本性的差异。它采用一对密钥，即公钥和私钥，分别用于加密和解密的过程。这两者密切相关，却拥有不同的功能。以下是对非对称加密体制基本原理的深入解析：

  1. 密钥对生成：用户通过数学算法生成一对非对称密钥，包括公钥和私钥。其中，公钥用于加密数据，私钥用于解密数据。
  2. 公钥传播：公钥具备自由传播的特性，因为它仅能用于加密数据。例如，用户A欲与用户B进行安全通信，A使用B的公钥加密数据，并将加密数据传送至B。
  3. 私钥保密：私钥则必须严格保密，只有密钥持有者可访问。私钥用于解密由公钥加密的数据，从而确保数据的机密性。
  4. 加密操作：发送方欲向接收方发送加密数据时，需使用接收方的公钥加密数据，以确保只有持有接收方私钥的人方可解密和阅读数据。
  5. 解密操作：接收方使用私钥解密数据。由于私钥仅由接收方知晓，这保障了只有接收方能够解密数据，从而保证了数据的完整性和机密性。
  6. 数字签名：非对称加密可用于数字签名。发送方可使用私钥对消息进行签名，而接收方则能够使用发送方的公钥验证签名的真实性，确保消息的来源和完整性。
  7. 密钥交换：非对称加密体制能够被应用于密钥交换。双方能够使用对方的公钥加密对称密钥并发送给对方。由于只有对方的私钥能够解密，因此双方能够安全地交换对称密钥，进而用于后续的加密和解密过程，提高效率。

非对称加密体制通过使用公钥和私钥提供更高级别的安全性，尤其适用于安全密钥交换和数字签名。然而，与对称加密相较，非对称加密运算速度较慢，通常需要与对称加密结合使用，以在实际应用中达到安全性和性能的有效平衡。

🛰?2.4.2 RES加密技术

RSA算法是一种非对称加密算法，广泛用于信息安全领域，包括数字签名、密钥交换和加密通信。RSA算法的安全性基于大整数分解的困难性，即在已知某数的乘积的情况下，难以找到它的因子。以下是RSA算法的详细介绍：

1. 密钥生成：

  • 选择两个大素数（p和q）：
    1. 随机选择两个大素数p和q。
    2. 计算它们的乘积n：n = p * q。
  • 计算欧拉函数φ(n)：
    • φ(n) = (p-1) * (q-1)
  • 选择公钥e：
    1. 选择一个整数e，满足1 < e < φ(n)且e与φ(n)互质。
    2. e成为公钥的一部分。
  • 计算私钥d：
    • 计算e关于φ(n)的模逆元d，即d * e ≡ 1 (mod φ(n))。
    • d成为私钥的一部分。
  • 公钥和私钥：
    • 公钥：(e, n)
    • 私钥：(d, n)

2. 加密过程：

  • 获取公钥(e, n)：
    • 发送方获取接收方的公钥。
  • 将明文转换为整数m：
    • 明文m需小于n。
  • 加密：
    • 计算密文c ≡ m^e (mod n)。
  • 发送密文：
    • 发送密文c给接收方。

3. 解密过程：

  • 获取私钥(d, n)：
    • 接收方使用自己的私钥。
  • 解密：
    • 计算明文m ≡ c^d (mod n)。
  • 将整数m转换为明文：
    • 将得到的整数m转换回明文。

4. 数字签名：

  • 签名过程：
    1. 发送方使用自己的私钥对消息的哈希值进行签名，得到签名s。
    2. 发送方将原始消息和签名发送给接收方。
  • 验证过程：
    1. 接收方使用发送方的公钥对签名进行解密，得到消息的哈希值。
    2. 接收方计算接收到的消息的哈希值。
    3. 如果两个哈希值匹配，则签名有效。

5. 密钥交换：

  • 发送方：
    1. 发送方使用接收方的公钥加密对称密钥。
    2. 发送方将加密后的对称密钥发送给接收方。
  • 接收方：
    1. 接收方使用自己的私钥解密对称密钥。
    2. 双方现在可以使用对称密钥进行加密和解密通信。

6. 安全性：

  • RSA的安全性基于大整数分解的困难性。
  • 安全性随着密钥长度的增加而提高，通常选择2048位或更长的密钥。

RSA算法为非对称加密提供了一种安全的解决方案，但由于其计算开销相对较高，通常与对称加密结合使用，以兼顾安全性和性能。

🛰?2.4.3 研究结果

JAVA代码：

import java.security.*;
import javax.crypto.*;

/**
 *	duichenjiami.java
 *
 *	This class creates a TripleDES key, encrypts some text,
 *	prints the ciphertext, then decrypts the text and
 *	prints that.
 *
 *	It requires a JCE-compliant TripleDES engine, like Cryptix' JCE.
 */
public class duichenjiami
{
  public static void main (String[] args)
  throws Exception
  {
    if (args.length != 1) {
      System.err.println("Usage: java duichenjiami text");
      System.exit(1);
    }
    String text = args[0];

    System.out.println("Generating a TripleDES key...");

    // Create a TripleDES key
    KeyGenerator keyGenerator = KeyGenerator.getInstance("TripleDES");
    keyGenerator.init(168);	// need to initialize with the keysize
    Key key = keyGenerator.generateKey();

    System.out.println("Done generating the key.");

    // Create a cipher using that key to initialize it
    Cipher cipher = Cipher.getInstance("TripleDES/ECB/PKCS5Padding");
    cipher.init(Cipher.ENCRYPT_MODE, key);

    byte[] plaintext = text.getBytes("UTF8");

    // Print out the bytes of the plaintext
    System.out.println("\nPlaintext: ");
    for (int i=0;i<plaintext.length;i++) {
		System.out.print(plaintext[i]+" ");
	}

    // Perform the actual encryption
    byte[] ciphertext = cipher.doFinal(plaintext);

	// Print out the ciphertext
    System.out.println("\n\nCiphertext: ");
    for (int i=0;i<ciphertext.length;i++) {
		System.out.print(ciphertext[i]+" ");
	}

    // Re-initialize the cipher to decrypt mode
    cipher.init(Cipher.DECRYPT_MODE, key);

    // Perform the decryption
    byte[] decryptedText = cipher.doFinal(ciphertext);

    String output = new String(decryptedText,"UTF8");

    System.out.println("\n\nDecrypted text: "+output);


  }
}

运行结果

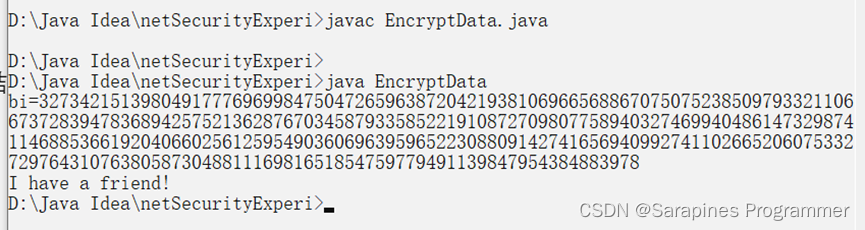
🕵??♂?2.5 研究记录

  • 非对称密钥体制基本概念：

    • 在实验中，清晰认识到非对称密钥体制与对称密钥体制的差异，其包含公钥和私钥，分别用于加密和解密。这种设计使得公钥能够公开，而私钥必须保密，提供了更高级别的安全性。

  • 实际操作深化理解：

    • 通过生成密钥对、加密和解密的实际操作，深入理解了非对称密钥体制相对于对称密钥体制的复杂性。尽管算法更为复杂，但也因此更难破解，为信息传输提供了可靠保障。

  • 数字签名的重要应用场景：

    • 学习了数字签名的概念和应用，了解其通过私钥签名和公钥验证的过程，有效确保信息的完整性和真实性。数字签名在信息交流中的身份验证和数据完整性保护方面具有重要作用，突显了非对称密钥体制的应用价值。

📝总结

🌐网络安全宛如一片汹涌激流，引领你豁然踏入数字领域的未知边界。这不是平凡的学习之旅，始于初级概念和实验布局，逐步启示更深层次的网络协议、编程魔法以及系统设计的神秘奥妙。

渴望迎接网络安全的学习挑战，征服数字世界的技术高峰？欢迎融入我们的社群，共同探讨更多可能性。我们倾心打造了备受瞩目的网络安全🔐 系列专栏?：《网络安全之道 | 数字征程》，旨在深度揭示网络安全技术的实战精髓和前沿创新。让我们一同翻开网络安全之谜的篇章，探索这个数字世界中的新奇可能性。🔍

文章来源:https://blog.csdn.net/m0_57532432/article/details/134877360
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。