MHF-Net(CVPR2019,TPAMI2020):一种可解释的光谱融合网络

MHF-Net

Paper：MHF-Net: An Interpretable Deep Network for Multispectral and Hyperspectral Image Fusion

Code：MHF-net: tpami，cvpr

简介

? 在光谱融合超分的领域中，现有传统方法极大依赖于手工先验知识，造成大量的主观性问题，而基于深度学习的方法，只是利用了通用图像超分的框架进行的处理，不具有很好的可解释性。

? 基于此，本论文从融合模型下手，通过将模型使用神经网络进行优化求解，让提出的MHF-net的每个模块都具有其自己的物理意义。在网络架构基础上，还针对训练数据和测试数据响应矩阵不匹配的问题进行了单独设计。

现阶段问题

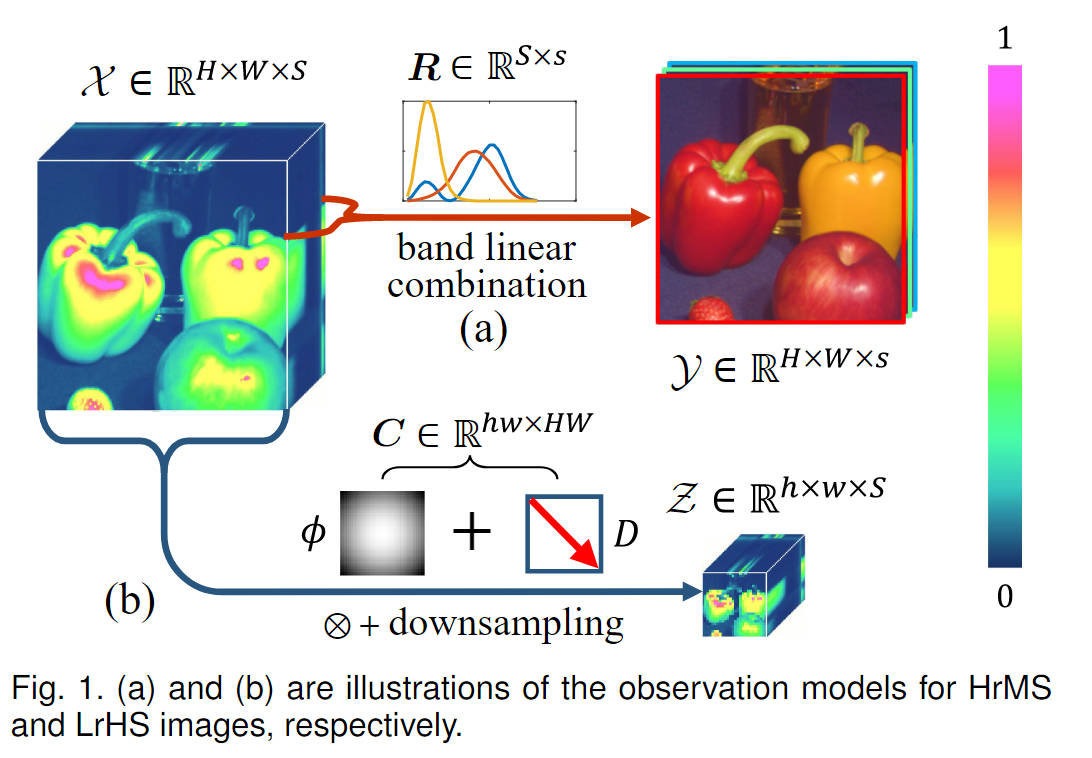
1. 即使已知R,C从退化的数据立方体转为三维数据立方体是ill-posed问题（不存在唯一解的问题）

   • 在传统的无监督方法中，有必要将X背后的先验结构数学编码为正则化器
   • 具体来说，在传统的无监督 MS/HS 融合方法中，通常需要在 X 上预先假设先验作为解决问题的正则化器,例如，早期的MS/HS融合技术继承了泛锐化原理，用小波级数展开[14]、[61]表示HS图像。然后，假设 HS 图像的空间信息可以在学习的字典 [2]、[15]、[63] 下稀疏表示，进一步利用 HS 图像上的空间稀疏表示来完成任务。此外，[31] 在 HrHS 图像上采用局部空间平滑度，并在他们的模型中使用总变化 (TV) 正则化。最近的一些方法不是从 HrHS 探索空间先验知识，而是假设 HrHS 上具有更多的内在光谱相关性，并采用低秩矩阵分解技术沿光谱 [54] [62] [30] 对此类先验进行编码。
   • 合理性依赖于手动强加于未知 HrHS 的先验假设来恢复,这些具有主观和相对简单的形式的手工先验总是不能充分和自适应地反映真实HSIs背后的内在复杂空间和光谱配置

2. 缺乏可解释性、偏离先验配置：

   • 现有的DL方法基本是通用超分架构，忽略了生成HrHS的内在理解，缺乏可解释性。
   • 忽略了一般HS图像明显拥有的先验知识结构，如光谱低秩性。这可能会导致网络输出偏离一般先验配置，从而影响恢复精度，

主要贡献

1. 充分考虑MS/HS融合的内在生成机制的DL方法，使用Y的完整基集进行计算，网络所有模块都具有可解释性

2. 考虑了训练和测试阶段响应不同的问题，将响应也作为网络输入进行模型的训练

---

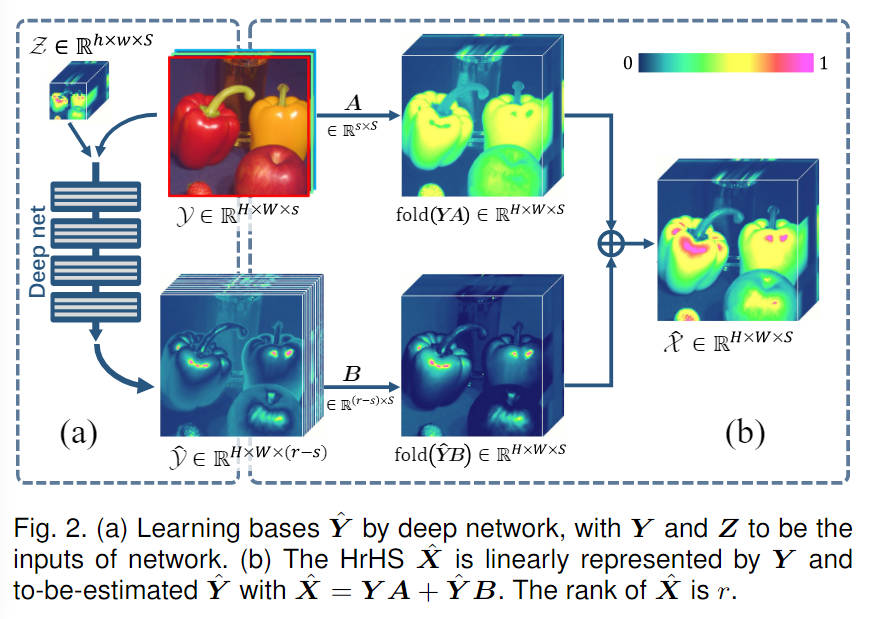
模型优化

$$Z=C(YA+\hat{Y}B)+N$$

设计优化问题：
$$\underset{\hat{\mathbf{Y}}}{\min }{\Vert C\left(YA+\hat{Y}B\right)?Z\Vert }_F^2+\lambda f\left(\hat{\mathbf{Y}}\right),$$
采用proximal gradient algorithm进行参数更新

其中$Q(\hat{Y},{\hat{Y}}^{(k)})$是二阶近似：$f(x)\approx f(x_0)+f^{\prime }(x_0)(x?x_0)+f^{\prime \prime }(x_0)\frac{(x?x_0{)}^2}{2}$
$$\begin{array}{rl}Q\left(\hat{\mathbf{Y}},{\hat{\mathbf{Y}}}^{(k)}\right)& =g\left({\hat{\mathbf{Y}}}^{(k)}\right)+?\hat{\mathbf{Y}}?{\hat{\mathbf{Y}}}^{(k)},?g\left({\hat{\mathbf{Y}}}^{(k)}\right)?\\ & +\frac{1}{2\eta }{\Vert \hat{Y}?{\hat{Y}}^{(k)}\Vert }_F^2+\lambda f\left(\hat{Y}\right),\end{array}$$
其中$g({\hat{Y}}^{(k)})=\Vert C(YA+{\hat{Y}}^{(k)}B)?Z{\Vert }_F^2$同时$\eta$作为步长的角色

A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems

根据上图，将优化问题转化为：
$$\underset{\hat{\mathbf{Y}}}{\min }\frac{1}{2}{\Vert \hat{\mathbf{Y}}?\left({\hat{\mathbf{Y}}}^{(k)}?\eta ?g\left({\hat{\mathbf{Y}}}^{(k)}\right)\right)\Vert }_F^2+\lambda \eta f\left(\hat{\mathbf{Y}}\right).$$
同时，其通解写为：
$${\hat{Y}}^{k+1}=pro{x}_{\lambda \eta }({\hat{\mathbf{Y}}}^{(k)}?\eta ?g({\hat{\mathbf{Y}}}^{(k)}))$$
又因为$?g({\hat{Y}}^{(k)})=C^T[C\left(YA+Y^{(k)}B?Z\right]B^T$

就可以将prox函数式子转为：
$${\hat{Y}}^{k+1}=pro{x}_{\lambda \eta }\left({\hat{\mathbf{Y}}}^{(k)}?\eta C^T\left(C\left(YA+Y^{(k)}B\right)?Z\right)B^T\right)$$

求解$?g({\hat{Y}}^{(k)})$

A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems

矩阵求导、几种重要的矩阵及常用的矩阵求导公式-CSDN博客

矩阵的 Frobenius 范数及其求偏导法则_f范数求导-CSDN博客

KaTeX parse error: Undefined control sequence: \tr at position 85: …=\operatorname{\?t?r?} \left( \left …

网络设计

? 由$X$是高分辨率图像，将其变为$E$为低分辨率图像，可以将$C$理解为一个下采样操作，反之$C^T$则为上采样操作，对于$pro{x}_{\lambda \eta }$可以将其看为一个复杂的仿射变换，比作一个神经网络操作。
$$\begin{array}{c}{X}^{(k)}=YA+{\hat{Y}}^{(k)}B,\\ E^{(k)}=C{X}^{(k)}?Z,\\ G^{(k)}=\eta C^T{E}^{(k)}{B}^T,\\ {\hat{\mathbf{Y}}}^{(k+1)}={\mathrm{prox}}_{\lambda \eta }\left({\hat{\mathbf{Y}}}^{(k)}?{\mathbf{G}}^{(k)}\right).\end{array}$$

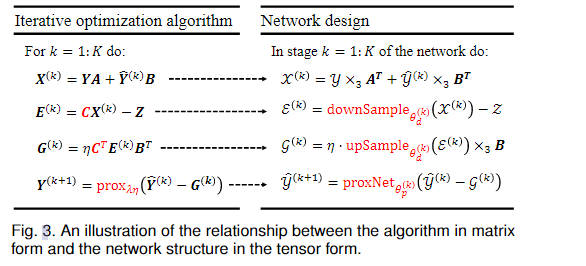
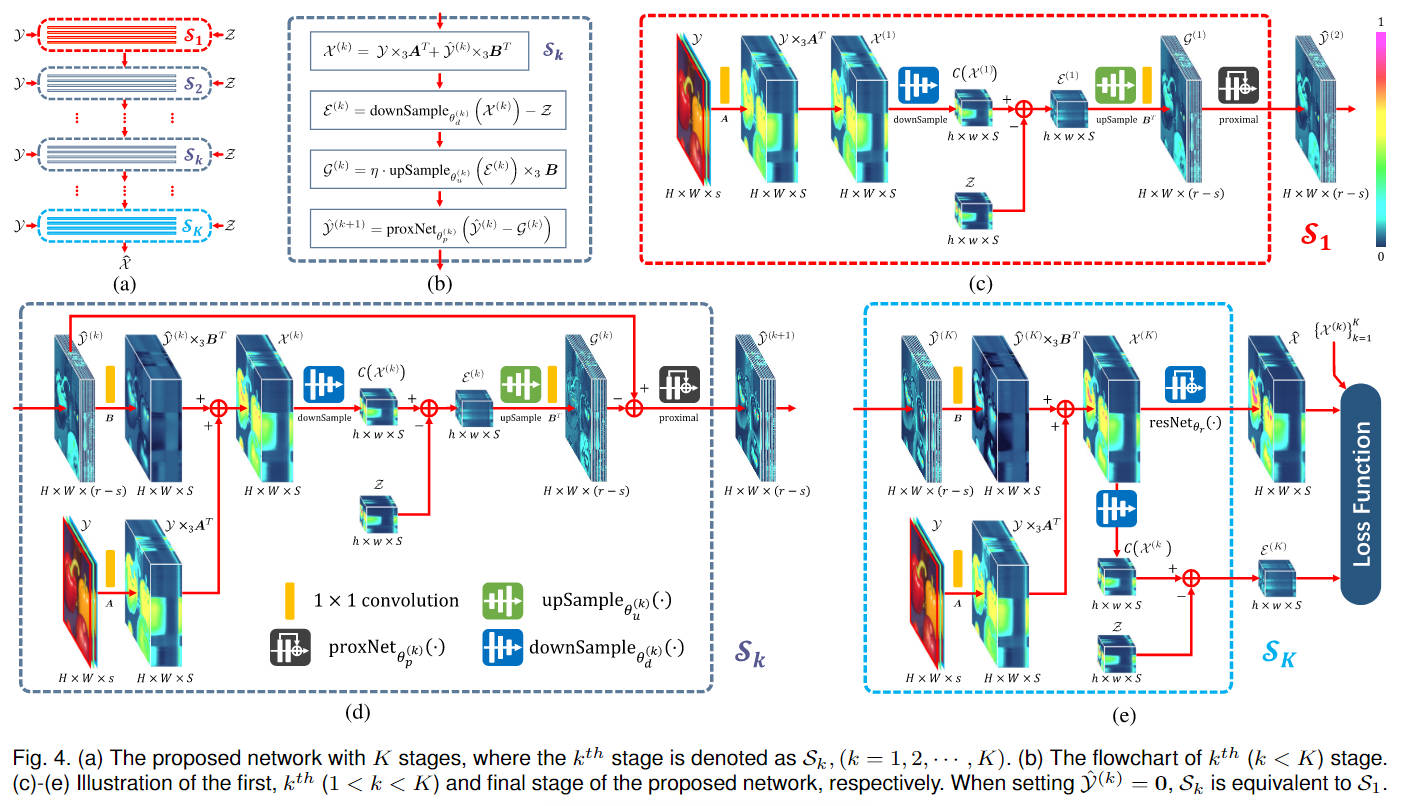
对于Blind Fusion NET的探索

? 将响应矩阵R,C的相关参数也作为模型的输入，其中A,B,C参数都可以从已有训练数据中通过基于模型的方法进行求解估计得到。

? 在训练过程中，对于每个训练样本进行参数估计，将其输入到模型进行训练。在测试阶段，同样是先进行参数估计，再进行输入。通过这种方式，网络有望捕获不同输入光谱和空间响应的一般恢复原理。

? 需要注意的是，此处网络在下采样和上采样过程中，不能简单使用原有的，需要根据求出的参数进行变化。

相关deep unrolling 文献

将优化问题转为神经网络进行求解

[1]W. Dong, P. Wang, W. Yin, G. Shi, F. Wu, and X. Lu, “Denoising Prior Driven Deep Neural Network for Image Restoration,” IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 2305–2318, Oct. 2019, doi: 10.1109/tpami.2018.2873610.

[1]L. Wang, C. Sun, Y. Fu, M. H. Kim, and H. Huang, “Hyperspectral Image Reconstruction Using a Deep Spatial-Spectral Prior,” in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, Jun. 2019. doi: 10.1109/cvpr.2019.00822.

[1]D. Yang and J. Sun, “Proximal Dehaze-Net: A Prior Learning-Based Deep Network for Single Image Dehazing,” in Computer Vision – ECCV 2018,Lecture Notes in Computer Science, 2018, pp. 729–746. doi: 10.1007/978-3-030-01234-2_43.

[1]Y. Yang, J. Sun, H. Li, and Z. Xu, “Deep ADMM-Net for compressive sensing MRI,” Neural Information Processing Systems,Neural Information Processing Systems, Dec. 2016.

[1]J. Zhang and B. Ghanem, “ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, Jun. 2018. doi: 10.1109/cvpr.2018.00196.

[1]J. Zhang, J. Pan, W.-S. Lai, RynsonW. H. Lau, and M.-H. Yang, “Learning Fully Convolutional Networks for Iterative Non-blind Deconvolution,” Cornell University - arXiv,Cornell University - arXiv, Nov. 2016.