大数据HCIE成神之路之数学（2）——线性代数

1.1 线性代数内容介绍

1.1.1 线性代数介绍

线性代数是一门被广泛运用于各工程技术领域的学科。用线性代数的相关概念和结论，可以极大地简化数据挖掘中相关公式的推导和表述。线性代数将复杂的问题简单化，让我们能够对问题进行高效地数学运算。

线性代数是一个数学工具，它不仅提供了有助于操作数组的技术，还提供了像向量和矩阵这样的数据结构用来保存数字和规则，以便进行加，减，乘，除的运算。

1.1.2 代码实现介绍

numpy是一款基于Python的数值处理模块，在处理矩阵数据方面有很强大的功能与优势。因为线性代数的主要内容就是对矩阵的处理，所以本章节主要的内容都是基于numpy进行展开。另外也会涉及到方程组求解，所以也会用到数学科学库scipy。

1.2 线性代数实现

导入相应库：

import numpy as np 
import scipy as sp 

1.2.1 reshape运算

在数学中并没有 reshape 运算，但是在numpy运算库中是一个非常常用的运算，用来改变一个张量的维度数和每个维度的大小，例如一个10x10的图片在保存时直接保存为一个包含100个元素的序列，在读取后就可以使用reshape将其从 1x100 变换为 10x10 。

示例如下：

生成一个包含整数0~11的向量

x = np.arange(12)
print(x)

结果输出：

[ 0  1  2  3  4  5  6  7  8  9 10 11]

注意：如果是直接np.arange(12)，输出结果为：

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

扩展学习：
如果是想要以逗号进行隔开方式打印x，则可以指定一下：

new_x = np.array2string(x, separator = ",")
print(new_x)

输出结果为：

[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11]

但是需要注意的是，此处打印的是str类型。

查看数组大小：

x.shape

结果输出：

(12,)

将x转换成二维矩阵，其中矩阵的第一个维度为1：

x = x.reshape(1,12)
print(x)

结果输出：

 [[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11]]

查看数组大小

x.shape

结果输出：

(1, 12)

将x转换3x4的矩阵

x = x.reshape(3,4)
print(x)

结果输出：

[[ 0,  1,  2,  3],
 [ 4,  5,  6,  7],
 [ 8,  9, 10, 11]]

1.2.2 转置实现

向量和矩阵的转置是交换行列顺序，而三维及以上张量的转置就需要指定转换的维度。

生成3*4的矩阵：

A = np.arange(12).reshape(3,4)
print(A)

结果输出：

[[ 0,  1,  2,  3],
 [ 4,  5,  6,  7],
 [ 8,  9, 10, 11]]

转置：

A.T

结果输出：

array([[ 0,  4,  8],
?        [ 1,  5,  9],
?        [ 2,  6, 10],
?        [ 3,  7, 11]])

1.2.3 矩阵乘法实现

矩阵乘法：记两个矩阵分别为A和B，两个矩阵能够相乘的条件为第一个矩阵的 列数 等于第二个矩阵的 行数 。

代码输入：

A = np.arange(6).reshape(3,2)
print(A)

结果输出：

[[0 1]
 [2 3]
 [4 5]]

B = np.arange(6).reshape(2,3)
print(B)

结果输出：

[[0, 1, 2],
 [3, 4, 5]]

矩阵相乘：

np.matmul(A,B)

注意：不要写成 A.matmul(B)，也不能写成 A*B 。
结果输出：

array([[ 3,  4,  5],
?       [ 9, 14, 19],
?       [15, 24, 33]])

1.2.4 矩阵对应运算

元素对应运算：针对形状相同矩阵的运算统称，包括元素对应相乘、相加等，即对两个矩阵相同位置的元素进行加减乘除等运算。

创建矩阵：

A = np.arange(6).reshape(3,2)

矩阵相乘：

print(A*A)

结果输出：

array([[ 0,  1],
?       [ 4,  9],
?       [16, 25]])

矩阵相加：

rint(A + A)

结果输出：

array([[ 0,  2],
?       [ 4,  6],
?       [ 8, 10]])

1.2.5 逆矩阵实现

只有方阵才有 逆矩阵 ，逆矩阵实现。

代码输入：

A = np.arange(4).reshape(2,2)
print(A)

结果输出：

array([[0, 1],
?       [2, 3]])

求逆矩阵：

np.linalg.inv(A)

结果输出：

array([[-1.5,  0.5],
?       [ 1. ,  0. ]])

注意：此处是 np.linalg ！不是scipy.linalg。可以自行了解如何求逆，此处不做过多解释。
提示：设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩B，使得： AB=BA=E 。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。其中，E为单位矩阵。

说明：
np.linalg 和 scipy.linalg 在提供线性代数函数方面有些重叠，但也存在一些区别。如果您只需要基本的线性代数功能，np.linalg足以满足您的需求。如果需要更高级的线性代数功能或特定的分解方法，您可能需要查看scipy.linalg中的函数。SciPy是建立在NumPy之上的科学计算库，提供了更广泛的数学、科学和工程计算功能。

如果是使用scipy的linalg

代码如下：

from scipy import linalg
linalg.inv(A)

输出结果为：

array([[-1.5,  0.5],
       [ 1. ,  0. ]])

1.2.6 特征值与特征向量

当谈论矩阵的 特征值 和 特征向量 时，我们首先需要了解 线性变换 和 向量空间 的概念。

• 线性变换是指将一个向量空间中的向量映射到另一个向量空间中的向量的操作。在二维平面上的旋转和缩放、三维空间中的投影等都是线性变换的例子。

• 向量空间是指由多个向量组成的集合，其中的向量可以进行加法和数乘运算。向量空间可以是二维平面、三维空间或更高维度的空间。

现在，我们来解释矩阵的特征值和特征向量：

• 特征值（Eigenvalues）是一个数值，表示线性变换作用后的向量在同一方向上的缩放倍数。当一个向量在经过线性变换后，只发生缩放而不改变方向时，这个缩放倍数就是特征值。

• 特征向量（Eigenvectors）是与特征值相关联的向量。它是表示在线性变换下保持在同一方向上的向量。特征向量不会改变方向，而是在线性变换后仅仅以特征值的倍数进行缩放。

具体来说，对于一个n维向量空间中的线性变换，我们可以表示为一个n×n的矩阵A。如果存在一个非零向量v和一个标量λ，使得下式成立：

A * v = λ * v

其中，v是 特征向量 ，λ是 特征值 。这意味着当矩阵A作用在特征向量v上时，结果只是将v进行了缩放，缩放的比例由特征值λ确定。

特征值和特征向量对于矩阵的理解和分析非常重要。它们提供了关于矩阵在线性变换过程中的行为和性质的信息。通过计算矩阵的特征值和特征向量，我们可以了解线性变换的缩放效果和主要方向，并在许多应用中提供有用的洞察力，如主成分分析、图像处理和振动分析等。

接下来进行求矩阵的 特征值 与 特征向量 并实现可视化。

导入相应库：

from scipy.linalg import eig
import numpy as np
import matplotlib.pyplot as plt

求特征值与特征向量：

A = [[1, 2],#生成一个2*2的矩阵
     [2, 1]] 
evals, evecs = eig(A) #求A的特征值（evals）和特征向量(evecs)
evecs = evecs[:, 0], evecs[:, 1]

plt.subplots() 返回一个Figure实例fig 和一个 AxesSubplot实例ax。fig代表整个图像，ax代表坐标轴和画的图。 作图：

fig, ax = plt.subplots()

输出图片如下：

让坐标轴经过原点：

for spine in ['left', 'bottom']:#让在左下角的坐标轴经过原点
    ax.spines[spine].set_position('zero')

画出网格：

ax.grid(alpha=0.4)

设置坐标轴的范围：

xmin, xmax = -3, 3
ymin, ymax = -3, 3
ax.set(xlim=(xmin, xmax), ylim=(ymin, ymax))

输出结果为：

[(-3.0, 3.0), (-3.0, 3.0)]

画出 特征向量 。用一个箭头指向要注释的地方，再写上一段话的行为，叫做annotate。text是输入内容；xy:箭头指向；xytext文字所处的位置；arrowprops通过arrowstyle表明箭头的风格或种类：

for v in evecs:
    ax.annotate(text="", xy=v, xytext=(0, 0),
                arrowprops=dict(facecolor='blue',
                shrink=0,
                alpha=0.6,
                width=0.5))

注意：
问题原因：annotate()的’s’参数自Matplotlib 3.3以后已重命名为’text’，不能使用s，不然会报错。

画出 特征空间 ：

x = np.linspace(xmin, xmax, 3)#在指定的间隔内返回均匀间隔的数字
for v in evecs:
    a = v[1] / v[0] #沿特征向量方向的单位向量
    ax.plot(x, a * x, 'r-', lw=0.4)# 参数 lw 表示图线的粗细
plt.show()  

可视化图像：

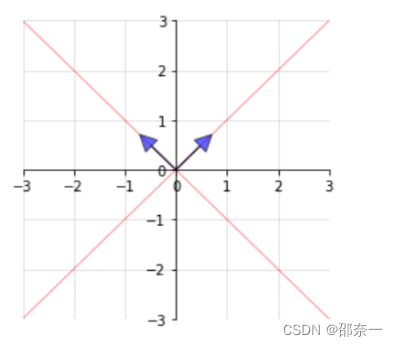
蓝箭头向量为特征向量，两条红色直线组成的空间为特征空间。

1.2.7 求行列式

求一个矩阵的行列式。

代码输入：

E = [[1, 2, 3],
      [4, 5, 6],
      [7, 8, 9]]
print(np.linalg.det(E))

np.linalg.det() 是NumPy库中的一个函数，用于计算矩阵的 行列式 。在这里，我们将矩阵E作为参数传递给np.linalg.det()函数

结果输出：

-9.51619735392994e-16

扩展阅读：
图说行列式：几张图让你明白行列式的性质
行列式的几何意义
总结：其实一个行列式的几何意义是有向线段(一阶行列式)或有向面积(二阶行列式)或有向体积(高阶行列式)。

1.2.8 奇异值分解实现

接下来利用奇异值分解（Singular Value Decomposition，SVD），通过文章标题出现的关键词，对文章进行聚类。

导入相应模块：

import numpy as np
import matplotlib.pyplot as plt

输入关键字：

words = ["books","dad","stock","value","singular","estate","decomposition"]

设已知8个标题，7个关键字。记录每个标题中每个关键字出现的次数，得矩阵X。 X中每一行表示一个标题，每一列表示一个关键字，矩阵中的每个元素表示一个关键字中一个标题中出现的次数。

X=np.array([[0,2,1,0,0,0,0],[2,0,0,1,0,1,0],[1,0,0,0,0,0,1],[0,0,1,0,0,0,0],[0,1,0,0,0,0,0],[0,0,0,1,1,0,1],[0,1,0,0,1,0,0],[0,0,0,0,1,1,1]])

进行奇异值分解：

U,s,Vh=np.linalg.svd(X)

输出左奇异矩阵U：

print("U=",U)

输出结果：

U= [[-1.87135757e-01 -7.93624528e-01  2.45011855e-01 -2.05404352e-01
  -3.88578059e-16  5.75779114e-16 -2.57394431e-01 -4.08248290e-01]
 [-6.92896814e-01  2.88368077e-01  5.67788037e-01  2.22142537e-01
   2.54000254e-01 -6.37019839e-16 -2.21623012e-02  2.05865892e-17]
 [-3.53233681e-01  1.22606651e-01  3.49203461e-02 -4.51735990e-01
  -7.62000762e-01  1.27403968e-15  2.72513448e-01  3.80488702e-17]
 [-2.61369658e-02 -1.33189110e-01  7.51079037e-02 -6.44727454e-01
   5.08000508e-01  1.77635684e-15  3.68146235e-01  4.08248290e-01]
 [-8.04993957e-02 -3.30217709e-01  8.49519758e-02  2.19661551e-01
  -2.54000254e-01 -4.81127681e-16 -3.12770333e-01  8.16496581e-01]
 [-3.95029694e-01  1.56123876e-02 -5.28290830e-01 -6.82340484e-02
   1.27000127e-01 -7.07106781e-01 -2.09360158e-01  1.55512464e-17]
 [-2.02089013e-01 -3.80395849e-01 -2.12899198e-01  4.80790894e-01
   8.04483689e-16 -1.60632798e-15  7.33466480e-01  1.76241226e-16]
 [-3.95029694e-01  1.56123876e-02 -5.28290830e-01 -6.82340484e-02
   1.27000127e-01  7.07106781e-01 -2.09360158e-01 -1.23226632e-16]]

输出奇异值矩阵：

print("s=",s)

按每个奇异值一一对应一个左奇异向量和一个右奇异向量奇异值从大到小排列输出结果：

s= [2.85653844 2.63792139 2.06449303 1.14829917 1.         1.
 0.54848559]

输出右奇异矩阵Vh：

print("Vh",Vh)

输出结果：

Vh [[-6.08788345e-01 -2.29949618e-01 -7.46612474e-02 -3.80854846e-01
  -3.47325416e-01 -3.80854846e-01 -4.00237243e-01]
 [ 2.65111314e-01 -8.71088358e-01 -3.51342402e-01  1.15234846e-01
  -1.32365989e-01  1.15234846e-01  5.83153945e-02]
 [ 5.66965547e-01  1.75382762e-01  1.55059743e-01  1.91316736e-02
  -6.14911671e-01  1.91316736e-02 -4.94872736e-01]
 [-6.48865369e-03  2.52237176e-01 -7.40339999e-01  1.34031699e-01
   2.99854608e-01  1.34031699e-01 -5.12239408e-01]
 [-2.54000254e-01 -2.54000254e-01  5.08000508e-01  3.81000381e-01
   2.54000254e-01  3.81000381e-01 -5.08000508e-01]
 [ 0.00000000e+00 -7.68640544e-16  2.33583082e-15 -7.07106781e-01
  -1.21802199e-15  7.07106781e-01  1.91457709e-15]
 [ 4.16034348e-01 -1.71550021e-01  2.01922906e-01 -4.22112199e-01
   5.73845817e-01 -4.22112199e-01 -2.66564648e-01]]

规定坐标轴的范围：

plt.axis([-0.8,0.2,-0.8,0.8])

输出图像为：

原每个关键字由 1*8 的向量表示，现降维成 1*2 的向量以便进行可视化

for i in range(len(words)):
    plt.text(U[i,0],U[i,1],words[i])
plt.show()

可视化结果：

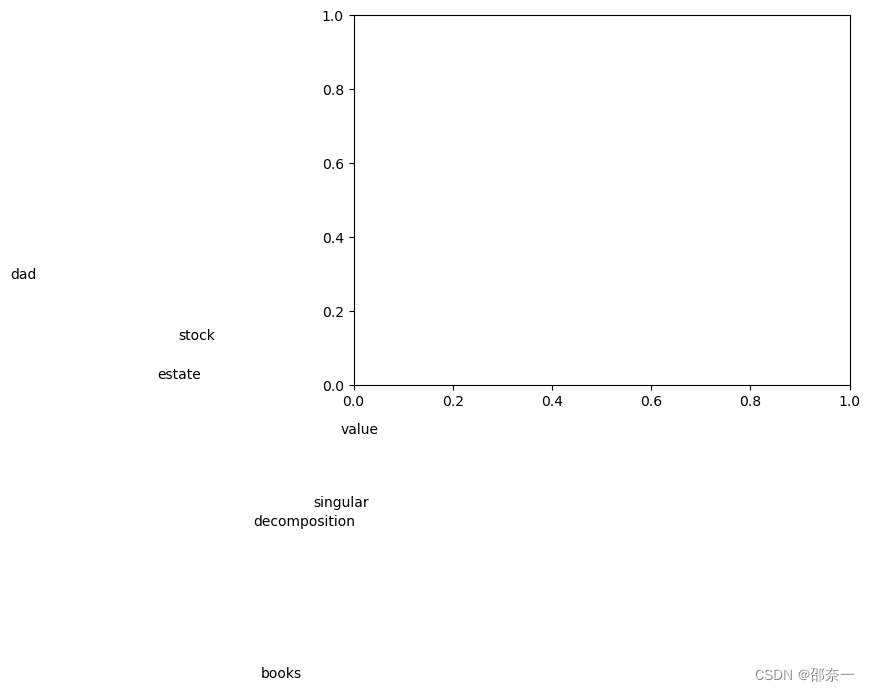
这张图是奇异值分解（SVD）的结果。奇异值分解是一种在线性代数中常用的矩阵分解方法，它将一个矩阵分解为三个矩阵的乘积，这三个矩阵分别代表了旋转、缩放和另一次旋转。在这张图中，每个点代表一个单词，它们的位置是通过奇异值分解得到的。这种分解方法可以帮助我们理解数据的结构和关系。

将到2维可视化后，我们可以将关键词聚类，如singular和decomposition距离比较近可以被划分为一组。

扩展阅读：
2分钟看懂奇异值分解
什么是奇异值分解SVD–SVD如何分解时空矩阵
补充：奇异值是特征值的开根。

1.2.9 线性方程组求解

求解线性方程组比较简单，只需要用到一个函数 scipy.linalg.solve() 就可以了。

比如我们对胶片中矩阵章节中的部门月度跑步案例进行线性方程组求解，线性方程组如下：

10x_1 + 8x_2 + 12x_3 = 20
4x_1 + 4x_2 + 2x_3 = 8
2x_1 - 4x_2- 2x_3 = -5

代码输入：

from scipy.linalg import solve
a = np.array([[10, 8, 12], [4, 4, 2], [2, -4, -2]])
b = np.array([20,8,-5])
x = solve(a, b)
print(x)

结果输出：

[0.5    1.3125 0.375 ]