Linear Regression线性回归(一元、多元)
2023-12-19 00:46:11
目录
介绍:?
线性回归是一种用于预测数值输出的统计分析方法。它通过建立自变量(也称为特征变量)和因变量之间的线性关系来进行预测。在线性回归中,自变量和因变量之间的关系可以用一条直线来表示。
线性回归的目标是找到最佳拟合直线,使得预测值和真实值之间的差异最小化。常用的求解方法是最小二乘法,即通过最小化预测值与真实值之间的平方差来确定最佳拟合直线的参数。
线性回归模型的表示形式如下:
Y = β0 + β1X1 + β2X2 + ... + βnXn + ε
其中,Y是因变量,X1到Xn是自变量,β0到βn是模型的参数,ε是误差项。
线性回归的优点包括模型简单易解释、计算效率高等。然而,线性回归的局限性在于它假设自变量和因变量之间的关系是线性的,如果真实关系是非线性的,线性回归可能无法提供准确的预测。此外,线性回归还对异常值和多重共线性敏感。
一、一元线性回归
1.1数据处理?
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression#应用Linear Regression线性回归 是个class
x=np.array([10,20,30,40,50,60])#自变量
y=np.array([15,45,50,70,110,130])#因变量
X=x.reshape(-1,1)
'''结果:
X array([[10],
[20],
[30],
[40],
[50],
[60]])
y array([ 15, 45, 50, 70, 110, 130]
'''
1.2建模
linreg.fit(X,y)#X和y赋给线性回归这个算法
y_predict=linreg.predict(X)#预测值
plt.scatter(X,y)#实际的点
plt.plot(X,y_predict,'Red')#线性回归这条线
plt.show()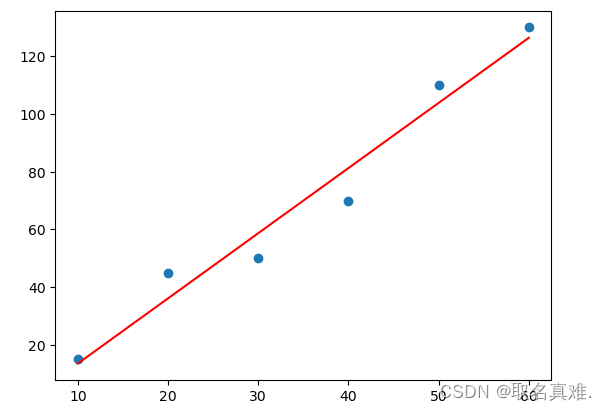
print(linreg.coef_)#斜率
#[2.25714286]
print(linreg.intercept_)#y轴的切入点
#-9.000000000000014?二、多元线性回归
2.1数据处理
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('50_Startups.csv')
dataset
'''结果:
R&D Spend Administration Marketing Spend State Profit
0 165349.20 136897.80 471784.10 New York 192261.83
1 162597.70 151377.59 443898.53 California 191792.06
2 153441.51 101145.55 407934.54 Florida 191050.39
3 144372.41 118671.85 383199.62 New York 182901.99
4 142107.34 91391.77 366168.42 Florida 166187.94
5 131876.90 99814.71 362861.36 New York 156991.12
6 134615.46 147198.87 127716.82 California 156122.51
7 130298.13 145530.06 323876.68 Florida 155752.60
8 120542.52 148718.95 311613.29 New York 152211.77
9 123334.88 108679.17 304981.62 California 149759.96
10 101913.08 110594.11 229160.95 Florida 146121.95
11 100671.96 91790.61 249744.55 California 144259.40
12 93863.75 127320.38 249839.44 Florida 141585.52
13 91992.39 135495.07 252664.93 California 134307.35
14 119943.24 156547.42 256512.92 Florida 132602.65
15 114523.61 122616.84 261776.23 New York 129917.04
16 78013.11 121597.55 264346.06 California 126992.93
17 94657.16 145077.58 282574.31 New York 125370.37
18 91749.16 114175.79 294919.57 Florida 124266.90
19 86419.70 153514.11 0.00 New York 122776.86
20 76253.86 113867.30 298664.47 California 118474.03
21 78389.47 153773.43 299737.29 New York 111313.02
22 73994.56 122782.75 303319.26 Florida 110352.25
23 67532.53 105751.03 304768.73 Florida 108733.99
24 77044.01 99281.34 140574.81 New York 108552.04
25 64664.71 139553.16 137962.62 California 107404.34
26 75328.87 144135.98 134050.07 Florida 105733.54
27 72107.60 127864.55 353183.81 New York 105008.31
28 66051.52 182645.56 118148.20 Florida 103282.38
29 65605.48 153032.06 107138.38 New York 101004.64
30 61994.48 115641.28 91131.24 Florida 99937.59
31 61136.38 152701.92 88218.23 New York 97483.56
32 63408.86 129219.61 46085.25 California 97427.84
33 55493.95 103057.49 214634.81 Florida 96778.92
34 46426.07 157693.92 210797.67 California 96712.80
35 46014.02 85047.44 205517.64 New York 96479.51
36 28663.76 127056.21 201126.82 Florida 90708.19
37 44069.95 51283.14 197029.42 California 89949.14
38 20229.59 65947.93 185265.10 New York 81229.06
39 38558.51 82982.09 174999.30 California 81005.76
40 28754.33 118546.05 172795.67 California 78239.91
41 27892.92 84710.77 164470.71 Florida 77798.83
42 23640.93 96189.63 148001.11 California 71498.49
43 15505.73 127382.30 35534.17 New York 69758.98
44 22177.74 154806.14 28334.72 California 65200.33
45 1000.23 124153.04 1903.93 New York 64926.08
46 1315.46 115816.21 297114.46 Florida 49490.75
47 0.00 135426.92 0.00 California 42559.73
48 542.05 51743.15 0.00 New York 35673.41
49 0.00 116983.80 45173.06 California 14681.40
'''X = dataset.iloc[:,0:4]#取前四列作为特征变量,第五行为y
y=dataset.iloc[:,4]#直接取第五列,为y值
X["State"].unique()#有几个不同的
#结果:array(['New York', 'California', 'Florida'], dtype=object
#因为State是类别性,需要进行加工,转化成数值
pd.get_dummies(X['State'])
'''结果:
California Florida New York
0 0 0 1
1 1 0 0
2 0 1 0
3 0 0 1
4 0 1 0
5 0 0 1
6 1 0 0
7 0 1 0
8 0 0 1
9 1 0 0
10 0 1 0
11 1 0 0
12 0 1 0
13 1 0 0
14 0 1 0
15 0 0 1
16 1 0 0
17 0 0 1
18 0 1 0
19 0 0 1
20 1 0 0
21 0 0 1
22 0 1 0
23 0 1 0
24 0 0 1
25 1 0 0
26 0 1 0
27 0 0 1
28 0 1 0
29 0 0 1
30 0 1 0
31 0 0 1
32 1 0 0
33 0 1 0
34 1 0 0
35 0 0 1
36 0 1 0
37 1 0 0
38 0 0 1
39 1 0 0
40 1 0 0
41 0 1 0
42 1 0 0
43 0 0 1
44 1 0 0
45 0 0 1
46 0 1 0
47 1 0 0
48 0 0 1
49 1 0 0
'''
statesdump=pd. get_dummies(X['State'],drop_first=True) #节省空间,florida和newyork为0就意味california
'''结果:
Florida New York
0 0 1
1 0 0
2 1 0
3 0 1
4 1 0
5 0 1
6 0 0
7 1 0
8 0 1
9 0 0
10 1 0
11 0 0
12 1 0
13 0 0
14 1 0
15 0 1
16 0 0
17 0 1
18 1 0
19 0 1
20 0 0
21 0 1
22 1 0
23 1 0
24 0 1
25 0 0
26 1 0
27 0 1
28 1 0
29 0 1
30 1 0
31 0 1
32 0 0
33 1 0
34 0 0
35 0 1
36 1 0
37 0 0
38 0 1
39 0 0
40 0 0
41 1 0
42 0 0
43 0 1
44 0 0
45 0 1
46 1 0
47 0 0
48 0 1
49 0 0
'''X=X.drop('State',axis=1)#去掉State那一列
X=pd.concat([X,statesdump],axis=1)#将statesdump加入
'''结果:
R&D Spend Administration Marketing Spend Florida New York
0 165349.20 136897.80 471784.10 0 1
1 162597.70 151377.59 443898.53 0 0
2 153441.51 101145.55 407934.54 1 0
3 144372.41 118671.85 383199.62 0 1
4 142107.34 91391.77 366168.42 1 0
5 131876.90 99814.71 362861.36 0 1
6 134615.46 147198.87 127716.82 0 0
7 130298.13 145530.06 323876.68 1 0
8 120542.52 148718.95 311613.29 0 1
9 123334.88 108679.17 304981.62 0 0
10 101913.08 110594.11 229160.95 1 0
11 100671.96 91790.61 249744.55 0 0
12 93863.75 127320.38 249839.44 1 0
13 91992.39 135495.07 252664.93 0 0
14 119943.24 156547.42 256512.92 1 0
15 114523.61 122616.84 261776.23 0 1
16 78013.11 121597.55 264346.06 0 0
17 94657.16 145077.58 282574.31 0 1
18 91749.16 114175.79 294919.57 1 0
19 86419.70 153514.11 0.00 0 1
20 76253.86 113867.30 298664.47 0 0
21 78389.47 153773.43 299737.29 0 1
22 73994.56 122782.75 303319.26 1 0
23 67532.53 105751.03 304768.73 1 0
24 77044.01 99281.34 140574.81 0 1
25 64664.71 139553.16 137962.62 0 0
26 75328.87 144135.98 134050.07 1 0
27 72107.60 127864.55 353183.81 0 1
28 66051.52 182645.56 118148.20 1 0
29 65605.48 153032.06 107138.38 0 1
30 61994.48 115641.28 91131.24 1 0
31 61136.38 152701.92 88218.23 0 1
32 63408.86 129219.61 46085.25 0 0
33 55493.95 103057.49 214634.81 1 0
34 46426.07 157693.92 210797.67 0 0
35 46014.02 85047.44 205517.64 0 1
36 28663.76 127056.21 201126.82 1 0
37 44069.95 51283.14 197029.42 0 0
38 20229.59 65947.93 185265.10 0 1
39 38558.51 82982.09 174999.30 0 0
40 28754.33 118546.05 172795.67 0 0
41 27892.92 84710.77 164470.71 1 0
42 23640.93 96189.63 148001.11 0 0
43 15505.73 127382.30 35534.17 0 1
44 22177.74 154806.14 28334.72 0 0
45 1000.23 124153.04 1903.93 0 1
46 1315.46 115816.21 297114.46 1 0
47 0.00 135426.92 0.00 0 0
48 542.05 51743.15 0.00 0 1
49 0.00 116983.80 45173.06 0 0
'''2.2数据分为训练集和测试集
from sklearn.model_selection import train_test_split#将数据分成测试和训练集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=0)#测试集占百分之三十,random_state=0随机抽取数据集里的成为测试集
X_train.count()
'''结果:
R&D Spend 35
Administration 35
Marketing Spend 35
Florida 35
New York 35
dtype: int64
'''
X_test.count()
'''结果:
R&D Spend 15
Administration 15
Marketing Spend 15
Florida 15
New York 15
dtype: int64
'''2.3建模
from sklearn.linear_model import LinearRegression
regressor=LinearRegression()
model=regressor.fit(X_train,y_train)#将训练集给到线性回归模型
y_predict=regressor.predict(X_test)#测试集因变量的预测值
from sklearn.metrics import r2_score
score1=r2_score(y_test,y_predict)#测试集的值与预测的值进行比较评估
score1#进行评估,越接近1,越好
#0.9358680970046241
model.coef_#参数,特征变量有五个,五元的线性回归
#结果:array([7.90840255e-01, 3.01968165e-02, 3.10148566e-02, #4.63028992e+02,3.04799573e+02])
model.score(X,y)#整个模型的值
#结果:0.9489303683771293
model.intercept_#y轴的切入
#结果:42403.8708705279
文章来源:https://blog.csdn.net/qq_74156152/article/details/135072699
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!