课题学习(十七)----姿态更新的四元数算法总结
?? 声明:因为接触本课题时间不长,对于四元数解法一直没太懂什么意思,本篇博客就对这几天的学习进行总结,肯定会有错误,希望读者能够帮忙指正。本篇博客主要参考秦永元老师《惯性导航》第九章第二小节以及几篇论文。
一、 四元数
1.1 四元数定义
?? 四元数就是由四个元构成的数:
Q
(
q
0
,
q
1
,
q
2
,
q
3
)
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
Q(q_0,q_1,q_2,q_3)=q_0+q_1\bold i+q_2\bold j+q_3\bold k
Q(q0?,q1?,q2?,q3?)=q0?+q1?i+q2?j+q3?k
??其中,
q
0
,
q
1
,
q
2
,
q
3
q_0,q_1,q_2,q_3
q0?,q1?,q2?,q3?是实数,在一些文献或者相关书籍里也会写作
q
1
,
q
2
,
q
3
,
q
4
q_1,q_2,q_3,q_4
q1?,q2?,q3?,q4?或者
w
,
x
,
y
,
z
w,x,y,z
w,x,y,z,
i
,
j
,
k
\bold i,\bold j,\bold k
i,j,k即是互相正交的向量,又是虚单位
?
1
\sqrt{-1}
?1?,具体规定体现在四元数乘法关系中:
i
?
i
=
?
1
,
j
?
j
=
?
1
,
k
?
k
=
?
1
\bold i\bigotimes \bold i=-1,\bold j\bigotimes \bold j=-1,\bold k\bigotimes \bold k=-1
i?i=?1,j?j=?1,k?k=?1
i
?
j
=
k
,
j
?
k
=
i
,
k
?
i
=
j
\bold i\bigotimes \bold j=\bold k,\bold j\bigotimes \bold k=\bold i,\bold k\bigotimes \bold i=\bold j
i?j=k,j?k=i,k?i=j
j
?
i
=
?
k
,
k
?
j
=
?
i
,
i
?
k
=
?
j
\bold j\bigotimes \bold i=-\bold k,\bold k\bigotimes \bold j=-\bold i,\bold i\bigotimes \bold k=-\bold j
j?i=?k,k?j=?i,i?k=?j
?? 上述公式符合 右手螺旋定则,可以绘制一个如下所示的三维图,用右手螺旋定则判断:
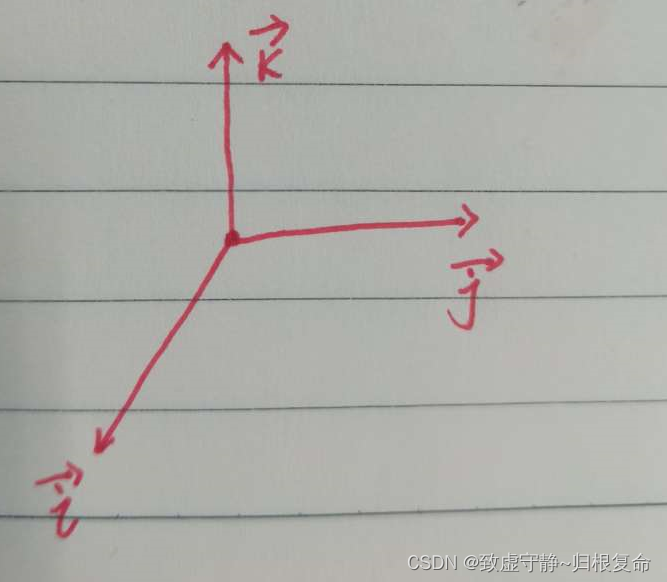
1.2 四元数的表示方法
?? (1)矢量式:
Q
=
q
0
+
q
Q = q_0+\bold q
Q=q0?+q
??(2)复数式:
Q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
Q=q_0+q_1\bold i+q_2\bold j+q_3\bold k
Q=q0?+q1?i+q2?j+q3?k
??(3)三角式:
Q
=
c
o
s
θ
2
+
u
s
i
n
θ
2
Q=cos \frac {\theta}{2}+\bold usin\frac {\theta}{2}
Q=cos2θ?+usin2θ?
??(4)指数式:
Q
=
e
u
θ
2
Q=e^{\bold u\frac {\theta}{2}}
Q=eu2θ?
??(5)矩阵式:
Q
=
[
q
0
q
1
q
2
q
3
]
Q=\begin{bmatrix}q_0\\q_1\\q_2\\q_3\end{bmatrix}
Q=
?q0?q1?q2?q3??
?
1.3 四元数大小----范数
?? 四元数的范数:
∣
∣
Q
∣
∣
=
q
0
2
+
q
1
2
+
q
2
2
+
q
3
2
||Q||=q_0^2+q_1^2+q_2^2+q_3^2
∣∣Q∣∣=q02?+q12?+q22?+q32?
??若
∣
∣
Q
∣
∣
=
1
||Q||=1
∣∣Q∣∣=1,则称为规范四元数。
1.4 四元数的加减乘除
?? (1)加法和减法:设
Q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
\bold Q=q_0+q_1\bold i+q_2\bold j+q_3\bold k
Q=q0?+q1?i+q2?j+q3?k
P
=
p
0
+
p
1
i
+
p
2
j
+
p
3
k
\bold P=p_0+p_1\bold i+p_2\bold j+p_3\bold k
P=p0?+p1?i+p2?j+p3?k
??则
Q
±
P
=
(
q
0
±
p
0
)
+
(
q
1
±
p
1
)
i
+
(
q
2
±
p
2
)
j
+
(
q
3
±
p
3
)
k
\bold Q±\bold P=(q_0±p_0)+(q_1±p_1)\bold i+(q_2±p_2)\bold j+(q_3±p_3)\bold k
Q±P=(q0?±p0?)+(q1?±p1?)i+(q2?±p2?)j+(q3?±p3?)k
??(2)乘法:
a
Q
=
a
q
0
+
a
q
1
i
+
a
q
2
j
+
a
q
3
k
a\bold Q=aq_0+aq_1\bold i+aq_2\bold j+aq_3\bold k
aQ=aq0?+aq1?i+aq2?j+aq3?k
P
?
Q
=
(
p
0
+
p
1
i
+
p
2
j
+
p
3
k
)
?
(
q
0
+
q
1
i
+
q
2
j
+
q
3
k
)
=
(
p
0
q
0
?
p
1
q
1
?
p
2
q
2
?
p
3
q
3
)
+
(
p
0
q
1
+
p
1
q
0
+
p
2
q
3
?
p
3
q
2
)
i
+
(
p
0
q
2
+
p
2
q
0
+
p
3
q
1
?
p
1
q
3
)
j
+
(
p
0
q
3
+
p
3
q
0
+
p
1
q
2
?
p
2
q
1
)
k
=
r
0
+
r
1
i
+
r
2
j
+
r
3
k
\bold P \bigotimes \bold Q =(p_0+p_1\bold i+p_2\bold j+p_3\bold k) \bigotimes (q_0+q_1\bold i+q_2\bold j+q_3\bold k)\\=(p_0q_0-p_1q_1-p_2q_2-p_3q_3)+(p_0q_1+p_1q_0+p_2q_3-p_3q_2)\bold i+\\(p_0q_2+p_2q_0+p_3q_1-p_1q_3)\bold j+(p_0q_3+p_3q_0+p_1q_2-p_2q_1)\bold k\\=r_0+r_1\bold i+r_2\bold j+r_3\bold k
P?Q=(p0?+p1?i+p2?j+p3?k)?(q0?+q1?i+q2?j+q3?k)=(p0?q0??p1?q1??p2?q2??p3?q3?)+(p0?q1?+p1?q0?+p2?q3??p3?q2?)i+(p0?q2?+p2?q0?+p3?q1??p1?q3?)j+(p0?q3?+p3?q0?+p1?q2??p2?q1?)k=r0?+r1?i+r2?j+r3?k
??上式写成矩阵:

??公式比较麻烦,就不敲了,记住一点就好, 四元数乘法不满足交换律。
??(3)求逆:
P
?
1
=
P
?
∣
∣
P
∣
∣
P^{-1}=\frac{P^*}{||P||}
P?1=∣∣P∣∣P??
二、四元数与姿态矩阵之间的关系
?? 秦老师的《惯性导航》在推导这部分时比较详细,推导部分这里就不再详细介绍了,主要讲一下几个重要的公式:
??《惯性导航》一书中取
u
R
=
[
l
m
n
]
\bold u^R=\begin{bmatrix}l\\m\\n\end{bmatrix}
uR=
?lmn?
? ,在薛启龙老师《Data Analytics for Drilling Engineering》的第三章“Dynamic Measurement of Spatial Attitude at the Bottom Rotating Drillstring”中,选择了
u
R
=
[
(
Θ
x
/
Θ
)
(
Θ
y
/
Θ
)
(
Θ
z
/
Θ
)
]
\bold u^R=\begin{bmatrix}(\Theta_x/\Theta)\\(\Theta_y/\Theta)\\(\Theta_z/\Theta)\end{bmatrix}
uR=
?(Θx?/Θ)(Θy?/Θ)(Θz?/Θ)?
? ,
Θ
x
/
Θ
、
Θ
y
/
Θ
、
Θ
z
/
Θ
\Theta_x/\Theta、\Theta_y/\Theta、\Theta_z/\Theta
Θx?/Θ、Θy?/Θ、Θz?/Θ是导航系中的方向余弦。
?? 姿态转换矩阵:
C
b
R
=
[
1
0
0
0
1
0
0
0
1
]
+
2
c
o
s
θ
2
[
0
?
n
s
i
n
θ
2
m
s
i
n
θ
2
n
s
i
n
θ
2
0
?
l
s
i
n
θ
2
?
m
s
i
n
θ
2
l
s
i
n
θ
2
0
]
+
2
[
?
(
m
2
+
n
2
)
s
i
n
2
θ
2
l
m
s
i
n
2
θ
2
l
n
s
i
n
2
θ
2
l
m
s
i
n
2
θ
2
?
(
l
2
+
n
2
)
s
i
n
2
θ
2
m
n
s
i
n
2
θ
2
l
n
s
i
n
2
θ
2
m
n
s
i
n
2
θ
2
?
(
m
2
+
n
2
)
s
i
n
2
θ
2
]
C_b^R=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}+2cos\frac{\theta}{2}\begin{bmatrix}0&-nsin\frac{\theta}{2}&msin\frac{\theta}{2}\\nsin\frac{\theta}{2}&0&-lsin\frac{\theta}{2}\\-msin\frac{\theta}{2}&lsin\frac{\theta}{2}&0\end{bmatrix}\\+2\begin{bmatrix}-(m^2+n^2)sin^2\frac{\theta}{2}&lmsin^2\frac{\theta}{2}&lnsin^2\frac{\theta}{2}\\lmsin^2\frac{\theta}{2}&-(l^2+n^2)sin^2\frac{\theta}{2}&mnsin^2\frac{\theta}{2}\\lnsin^2\frac{\theta}{2}&mnsin^2\frac{\theta}{2}&-(m^2+n^2)sin^2\frac{\theta}{2}\end{bmatrix}
CbR?=
?100?010?001?
?+2cos2θ?
?0nsin2θ??msin2θ???nsin2θ?0lsin2θ??msin2θ??lsin2θ?0?
?+2
??(m2+n2)sin22θ?lmsin22θ?lnsin22θ??lmsin22θ??(l2+n2)sin22θ?mnsin22θ??lnsin22θ?mnsin22θ??(m2+n2)sin22θ??
?
??简化上式,令:
{
q
0
=
c
o
s
θ
2
q
1
=
l
s
i
n
θ
2
q
2
=
m
s
i
n
θ
2
q
3
=
n
s
i
n
θ
2
\begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases}
?
?
??q0?=cos2θ?q1?=lsin2θ?q2?=msin2θ?q3?=nsin2θ??
??
∣
∣
Q
∣
∣
=
q
0
2
+
q
1
2
+
q
2
2
+
q
3
2
=
1
||Q||=q_0^2+q_1^2+q_2^2+q_3^2=1
∣∣Q∣∣=q02?+q12?+q22?+q32?=1,为规范四元数,并且以
q
0
,
q
1
,
q
2
,
q
3
q_0,q_1,q_2,q_3
q0?,q1?,q2?,q3?构造四元数:
Q
=
c
o
s
θ
2
+
u
R
s
i
n
θ
2
Q=cos\frac{\theta}{2}+\bold u^Rsin\frac{\theta}{2}
Q=cos2θ?+uRsin2θ?
??(1)物理意义: 绕参考坐标系R内的一个的单位向量
u
?
\vec u
u转动角度
θ
\theta
θ,注意:不是转动
θ
2
\frac{\theta}{2}
2θ?!!!
??(2)四元数可以确定b系至R(R是参考坐标系,一般选择导航坐标系n)系的姿态转换矩阵:
C
b
R
=
[
1
?
2
(
q
2
2
+
q
3
2
)
2
(
q
1
q
2
?
q
3
q
0
)
2
(
q
1
q
3
+
q
2
q
0
)
2
(
q
1
q
2
+
q
3
q
0
)
1
?
2
(
q
1
2
+
q
3
2
)
2
(
q
2
q
3
?
q
1
q
0
)
2
(
q
1
q
3
?
q
2
q
0
)
2
(
q
2
q
3
+
q
1
q
0
)
1
?
(
q
1
2
+
q
3
2
)
]
C_b^R=\begin{bmatrix} 1-2(q^2_{2}+q^2_{3}) &2(q_{1}q_{2}-q_{3}q_{0})&2(q_{1}q_{3}+q_{2}q_{0})\\ 2(q_{1}q_{2}+q_{3}q_{0}) &1-2(q^2_{1}+q^2_{3})&2(q_{2}q_{3}-q_{1}q_{0})\\ 2(q_{1}q_{3}-q_{2}q_{0})&2(q_{2}q_{3}+q_{1}q_{0})&1-(q^2_{1}+q^2_{3}) \end{bmatrix}
CbR?=
?1?2(q22?+q32?)2(q1?q2?+q3?q0?)2(q1?q3??q2?q0?)?2(q1?q2??q3?q0?)1?2(q12?+q32?)2(q2?q3?+q1?q0?)?2(q1?q3?+q2?q0?)2(q2?q3??q1?q0?)1?(q12?+q32?)?
?
?? 由于是规范四元数,也可以写作下式
C
b
R
=
[
q
1
2
?
q
2
2
?
q
3
2
+
q
0
2
2
(
q
1
q
2
?
q
3
q
0
)
2
(
q
1
q
3
+
q
2
q
0
)
2
(
q
1
q
2
+
q
3
q
0
)
?
q
1
2
+
q
2
2
?
q
3
2
+
q
0
2
2
(
q
2
q
3
?
q
1
q
0
)
2
(
q
1
q
3
?
q
2
q
0
)
2
(
q
2
q
3
+
q
1
q
0
)
?
q
1
2
?
q
2
2
+
q
3
2
+
q
0
2
]
C_b^R=\begin{bmatrix} q^2_{1}-q^2_{2}-q^2_{3}+q^2_{0} &2(q_{1}q_{2}-q_{3}q_{0})&2(q_{1}q_{3}+q_{2}q_{0})\\ 2(q_{1}q_{2}+q_{3}q_{0}) &-q^2_{1}+q^2_{2}-q^2_{3}+q^2_{0}&2(q_{2}q_{3}-q_{1}q_{0})\\ 2(q_{1}q_{3}-q_{2}q_{0})&2(q_{2}q_{3}+q_{1}q_{0})&-q^2_{1}-q^2_{2}+q^2_{3}+q^2_{0} \end{bmatrix}
CbR?=
?q12??q22??q32?+q02?2(q1?q2?+q3?q0?)2(q1?q3??q2?q0?)?2(q1?q2??q3?q0?)?q12?+q22??q32?+q02?2(q2?q3?+q1?q0?)?2(q1?q3?+q2?q0?)2(q2?q3??q1?q0?)?q12??q22?+q32?+q02??
?
??(3)如果把
r
R
、
r
b
\bold r^R、\bold r^b
rR、rb看做是零标量的四元数,那么他们之间的变换关系可以采用四元数乘法表示:
r
R
=
Q
?
r
b
?
Q
?
\bold r^R=\bold Q\bigotimes\bold r^b\bigotimes\bold Q^*
rR=Q?rb?Q?
??该式称为坐标变换的四元数乘表示法
??设参考坐标系为导航坐标系n,设航向角为
Ψ
\Psi
Ψ,俯仰角为
θ
\theta
θ,横滚角为
γ
\gamma
γ:
C
b
n
=
[
c
o
s
Ψ
c
o
s
γ
+
s
i
n
Ψ
s
i
n
θ
s
i
n
γ
s
i
n
Ψ
c
o
s
θ
c
o
s
Ψ
c
o
s
γ
?
s
i
n
Ψ
s
i
n
θ
c
o
s
γ
?
s
i
n
Ψ
c
o
s
γ
+
c
o
s
Ψ
s
i
n
θ
s
i
n
γ
c
o
s
Ψ
c
o
s
θ
?
s
i
n
Ψ
s
i
n
γ
?
c
o
s
Ψ
s
i
n
θ
c
o
s
γ
?
c
o
s
θ
s
i
n
γ
s
i
n
θ
c
o
s
θ
c
o
s
γ
]
=
[
T
11
T
12
T
13
T
21
T
22
T
23
T
31
T
32
T
33
]
C_b^n=\begin{bmatrix} cos\Psi cos\gamma+sin\Psi sin\theta sin\gamma&sin\Psi cos\theta &cos\Psi cos\gamma-sin\Psi sin\theta cos\gamma\\ -sin\Psi cos\gamma+cos\Psi sin\theta sin\gamma&cos\Psi cos\theta &-sin\Psi sin\gamma-cos\Psi sin\theta cos\gamma\\ -cos\theta sin\gamma&sin\theta &cos\theta cos\gamma\end{bmatrix}\\=\begin{bmatrix}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{bmatrix}
Cbn?=
?cosΨcosγ+sinΨsinθsinγ?sinΨcosγ+cosΨsinθsinγ?cosθsinγ?sinΨcosθcosΨcosθsinθ?cosΨcosγ?sinΨsinθcosγ?sinΨsinγ?cosΨsinθcosγcosθcosγ?
?=
?T11?T21?T31??T12?T22?T32??T13?T23?T33??
?
??下图为姿态角的真值表:
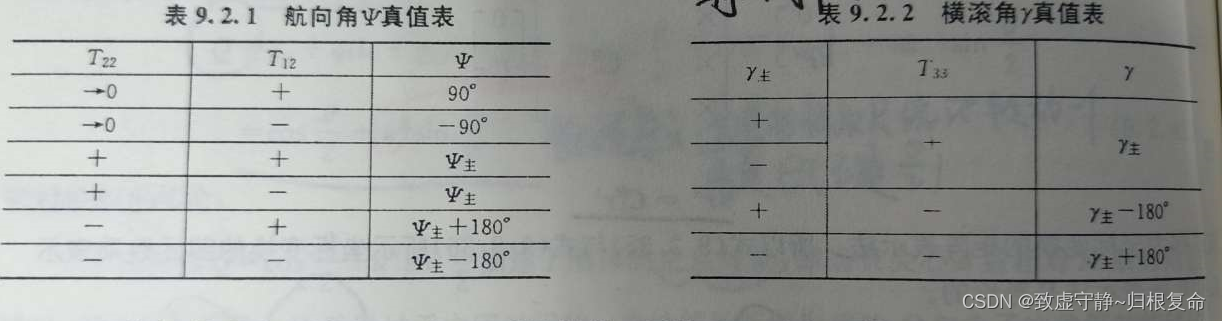
??经过上述的分析:如果旋转四元数
Q
\bold Q
Q已经确定,那么就可以表示出
C
b
n
C_b^n
Cbn?:
C
b
n
=
[
q
1
2
?
q
2
2
?
q
3
2
+
q
0
2
2
(
q
1
q
2
?
q
3
q
0
)
2
(
q
1
q
3
+
q
2
q
0
)
2
(
q
1
q
2
+
q
3
q
0
)
?
q
1
2
+
q
2
2
?
q
3
2
+
q
0
2
2
(
q
2
q
3
?
q
1
q
0
)
2
(
q
1
q
3
?
q
2
q
0
)
2
(
q
2
q
3
+
q
1
q
0
)
?
q
1
2
?
q
2
2
+
q
3
2
+
q
0
2
]
=
[
M
11
M
12
M
13
M
21
M
22
M
23
M
31
M
32
M
33
]
C_b^n=\begin{bmatrix} q^2_{1}-q^2_{2}-q^2_{3}+q^2_{0} &2(q_{1}q_{2}-q_{3}q_{0})&2(q_{1}q_{3}+q_{2}q_{0})\\ 2(q_{1}q_{2}+q_{3}q_{0}) &-q^2_{1}+q^2_{2}-q^2_{3}+q^2_{0}&2(q_{2}q_{3}-q_{1}q_{0})\\ 2(q_{1}q_{3}-q_{2}q_{0})&2(q_{2}q_{3}+q_{1}q_{0})&-q^2_{1}-q^2_{2}+q^2_{3}+q^2_{0} \end{bmatrix}\\=\begin{bmatrix}M_{11}&M_{12}&M_{13}\\M_{21}&M_{22}&M_{23}\\M_{31}&M_{32}&M_{33}\end{bmatrix}
Cbn?=
?q12??q22??q32?+q02?2(q1?q2?+q3?q0?)2(q1?q3??q2?q0?)?2(q1?q2??q3?q0?)?q12?+q22??q32?+q02?2(q2?q3?+q1?q0?)?2(q1?q3?+q2?q0?)2(q2?q3??q1?q0?)?q12??q22?+q32?+q02??
?=
?M11?M21?M31??M12?M22?M32??M13?M23?M33??
?
??与基本旋转之后的转换矩阵对比,即可解算出姿态:
C
b
n
=
[
c
o
s
Ψ
c
o
s
γ
+
s
i
n
Ψ
s
i
n
θ
s
i
n
γ
s
i
n
Ψ
c
o
s
θ
c
o
s
Ψ
c
o
s
γ
?
s
i
n
Ψ
s
i
n
θ
c
o
s
γ
?
s
i
n
Ψ
c
o
s
γ
+
c
o
s
Ψ
s
i
n
θ
s
i
n
γ
c
o
s
Ψ
c
o
s
θ
?
s
i
n
Ψ
s
i
n
γ
?
c
o
s
Ψ
s
i
n
θ
c
o
s
γ
?
c
o
s
θ
s
i
n
γ
s
i
n
θ
c
o
s
θ
c
o
s
γ
]
=
[
T
11
T
12
T
13
T
21
T
22
T
23
T
31
T
32
T
33
]
C_b^n=\begin{bmatrix} cos\Psi cos\gamma+sin\Psi sin\theta sin\gamma&sin\Psi cos\theta &cos\Psi cos\gamma-sin\Psi sin\theta cos\gamma\\ -sin\Psi cos\gamma+cos\Psi sin\theta sin\gamma&cos\Psi cos\theta &-sin\Psi sin\gamma-cos\Psi sin\theta cos\gamma\\ -cos\theta sin\gamma&sin\theta &cos\theta cos\gamma\end{bmatrix}\\=\begin{bmatrix}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{bmatrix}
Cbn?=
?cosΨcosγ+sinΨsinθsinγ?sinΨcosγ+cosΨsinθsinγ?cosθsinγ?sinΨcosθcosΨcosθsinθ?cosΨcosγ?sinΨsinθcosγ?sinΨsinγ?cosΨsinθcosγcosθcosγ?
?=
?T11?T21?T31??T12?T22?T32??T13?T23?T33??
?
?? 一定注意的是,
C
b
n
、
C
n
b
C_b^n、 C_n^b
Cbn?、Cnb?矩阵存在着转置的关系!!!计算时一定要注意!!!
??例如,求解
θ
\theta
θ时可以用
C
n
b
C_n^b
Cnb?中可以第二列求解,即
θ
=
a
r
c
t
a
n
(
s
i
n
θ
(
s
i
n
Ψ
c
o
s
θ
)
2
+
(
c
o
s
Ψ
c
o
s
θ
)
2
)
\theta=arctan(\frac{sin\theta}{\sqrt{(sin\Psi cos\theta)^2+(cos\Psi cos\theta)^2}})
θ=arctan((sinΨcosθ)2+(cosΨcosθ)2?sinθ?),也就是
θ
=
a
r
c
t
a
n
(
T
32
T
12
2
+
T
22
2
)
\theta=arctan(\frac{T_{32}}{\sqrt{T_{12}^2+T_{22}^2}})
θ=arctan(T122?+T222??T32??),由于知道了四元素构成的
C
b
n
C_b^n
Cbn?,那么
θ
=
a
r
c
t
a
n
(
M
32
M
12
2
+
M
22
2
)
\theta=arctan(\frac{M_{32}}{\sqrt{M_{12}^2+M_{22}^2}})
θ=arctan(M122?+M222??M32??) ,这就是最终的计算公式。
??下面是我的代码中使用的姿态解算公式:
gyro_var->euler.pit = (asin(2*q2q3 + 2*q0q1))*57.29578f;
gyro_var->euler.roll = (atan2(-2*q1q3 + 2*q0q2, -2*q1q1-2*q2q2 + 1))*57.29578f;
gyro_var->euler.yaw = (atan2(2*q1q2 - 2*q0q3, -2*q2q2-2*q3q3+1))*57.29578f;
三、四元数微分方程
?? 令
ω
R
b
b
=
[
ω
x
ω
y
ω
z
]
\omega_{Rb}^b=\begin{bmatrix}\omega_x\\\omega_y\\\omega_z\end{bmatrix}
ωRbb?=
?ωx?ωy?ωz??
?,
d
Q
d
t
=
1
2
M
′
(
ω
R
b
b
)
Q
\frac{d\bold Q}{dt}=\frac{1}{2}\bold M'(\omega_{Rb}^b)\bold Q
dtdQ?=21?M′(ωRbb?)Q
??即
[
q
˙
0
q
˙
1
q
˙
2
q
˙
3
]
=
1
2
[
0
?
ω
x
?
ω
y
?
ω
z
ω
x
0
ω
z
?
ω
y
ω
y
?
ω
z
0
ω
x
ω
z
ω
y
?
ω
x
0
]
[
q
0
q
1
q
2
q
3
]
\begin{bmatrix}\dot q_0\\\dot q_1\\\dot q_2\\\dot q_3\end{bmatrix}=\frac{1}{2}\begin{bmatrix}0&-\omega_x&-\omega_y&-\omega_z\\ \omega_x&0&\omega_z&-\omega_y\\ \omega_y&-\omega_z&0&\omega_x\\ \omega_z&\omega_y&-\omega_x&0 \end{bmatrix} \begin{bmatrix} q_0\\q_1\\ q_2\\ q_3\end{bmatrix}
?q˙?0?q˙?1?q˙?2?q˙?3??
?=21?
?0ωx?ωy?ωz???ωx?0?ωz?ωy???ωy?ωz?0?ωx???ωz??ωy?ωx?0?
?
?q0?q1?q2?q3??
?
??
ω
n
b
b
\omega_{nb}^b
ωnbb?可以使用
ω
n
b
b
=
ω
i
b
b
?
C
n
b
(
ω
i
e
n
+
ω
e
n
n
)
\omega_{nb}^b=\omega_{ib}^b-C_n^b(\omega_{ie}^n+\omega_{en}^n)
ωnbb?=ωibb??Cnb?(ωien?+ωenn?)公式计算,
ω
i
b
b
\omega_{ib}^b
ωibb?是陀螺仪的输出(对陀螺仪必须经过动、静态误差的补偿),
ω
i
e
n
、
ω
e
n
n
\omega_{ie}^n、\omega_{en}^n
ωien?、ωenn?分别是 位置速率和地球自转速率:
ω
i
e
n
+
ω
e
n
n
=
(
?
V
N
R
M
V
E
R
N
+
ω
i
e
c
o
s
L
V
E
t
a
n
L
R
N
+
ω
i
e
s
i
n
L
)
\omega_{ie}^n+\omega_{en}^n=\begin{pmatrix}\frac{-V_N}{R_M}\\ \frac{V_E}{R_N}+\omega_{ie}cosL \\ \frac{V_{E}tanL}{R_N}+\omega_{ie}sinL \end{pmatrix}
ωien?+ωenn?=
?RM??VN??RN?VE??+ωie?cosLRN?VE?tanL?+ωie?sinL?
?
??秦老师在第七章介绍了上式的一些定义:
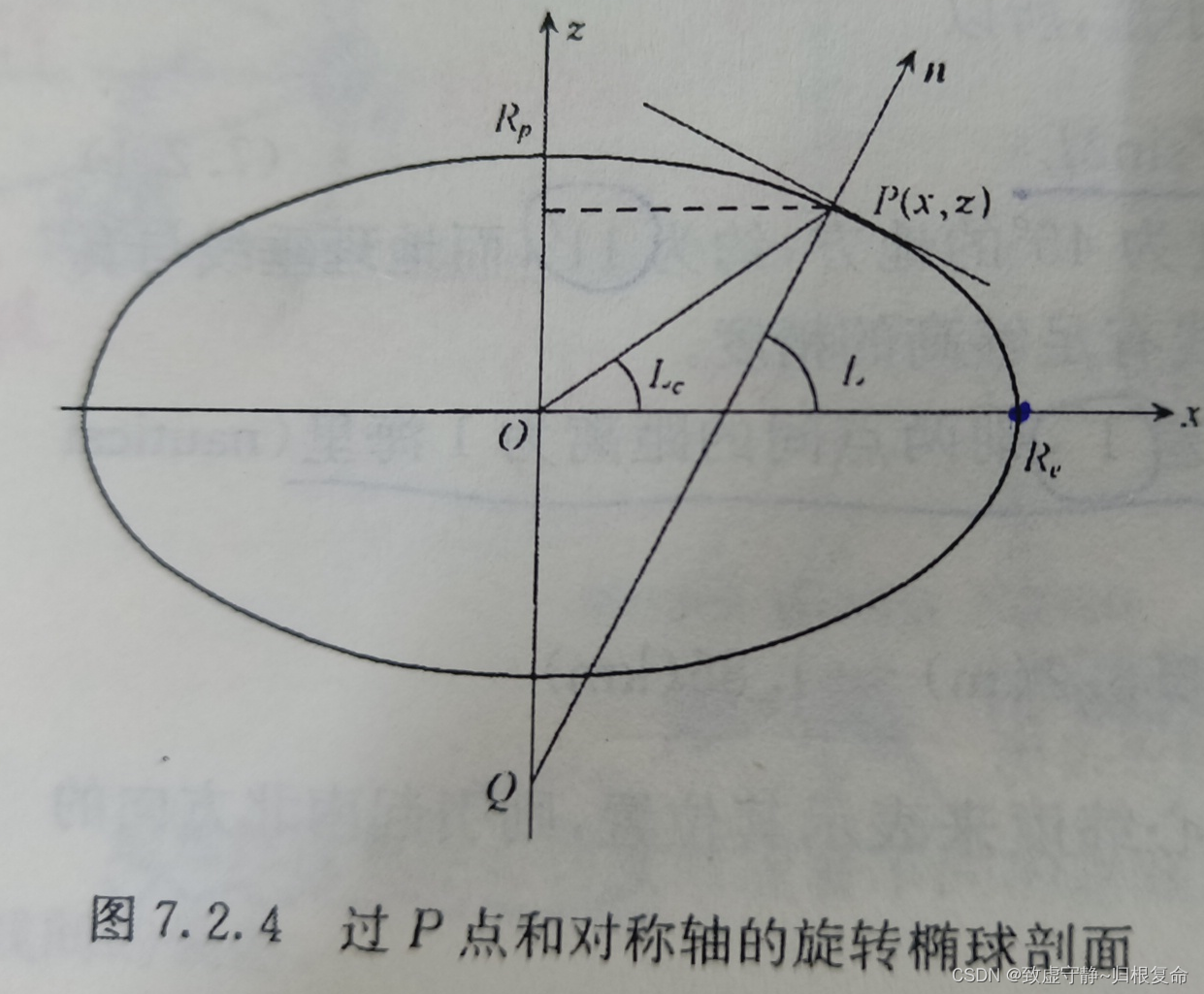
??
L
L
L为地理纬度,
R
M
,
R
N
R_M,R_N
RM?,RN?分别是沿子午圈和沿卯酉圈的曲率半径:
R
M
=
R
e
(
1
?
f
)
2
[
1
?
(
2
?
f
)
s
i
n
2
L
]
?
3
2
R_M=R_e(1-f)^2[1-(2-f)sin^2L]^{-\frac{3}{2}}
RM?=Re?(1?f)2[1?(2?f)sin2L]?23?
R
N
=
R
e
[
1
?
(
2
?
f
)
s
i
n
2
L
]
?
1
2
R_N=R_e[1-(2-f)sin^2L]^{-\frac{1}{2}}
RN?=Re?[1?(2?f)sin2L]?21?
??
R
e
R_e
Re?是地球(椭圆)的长轴,
R
p
R_p
Rp?是地球(椭圆)的短轴,
R
p
=
(
1
?
f
)
R
e
R_p=(1-f)R_e
Rp?=(1?f)Re? 。
四、四元数微分方程的毕卡求解法
?? 这里只介绍一下定时采样增量法,主要是通过对
Q
Q
Q进行泰勒展开,对四元数进行各阶的近似:
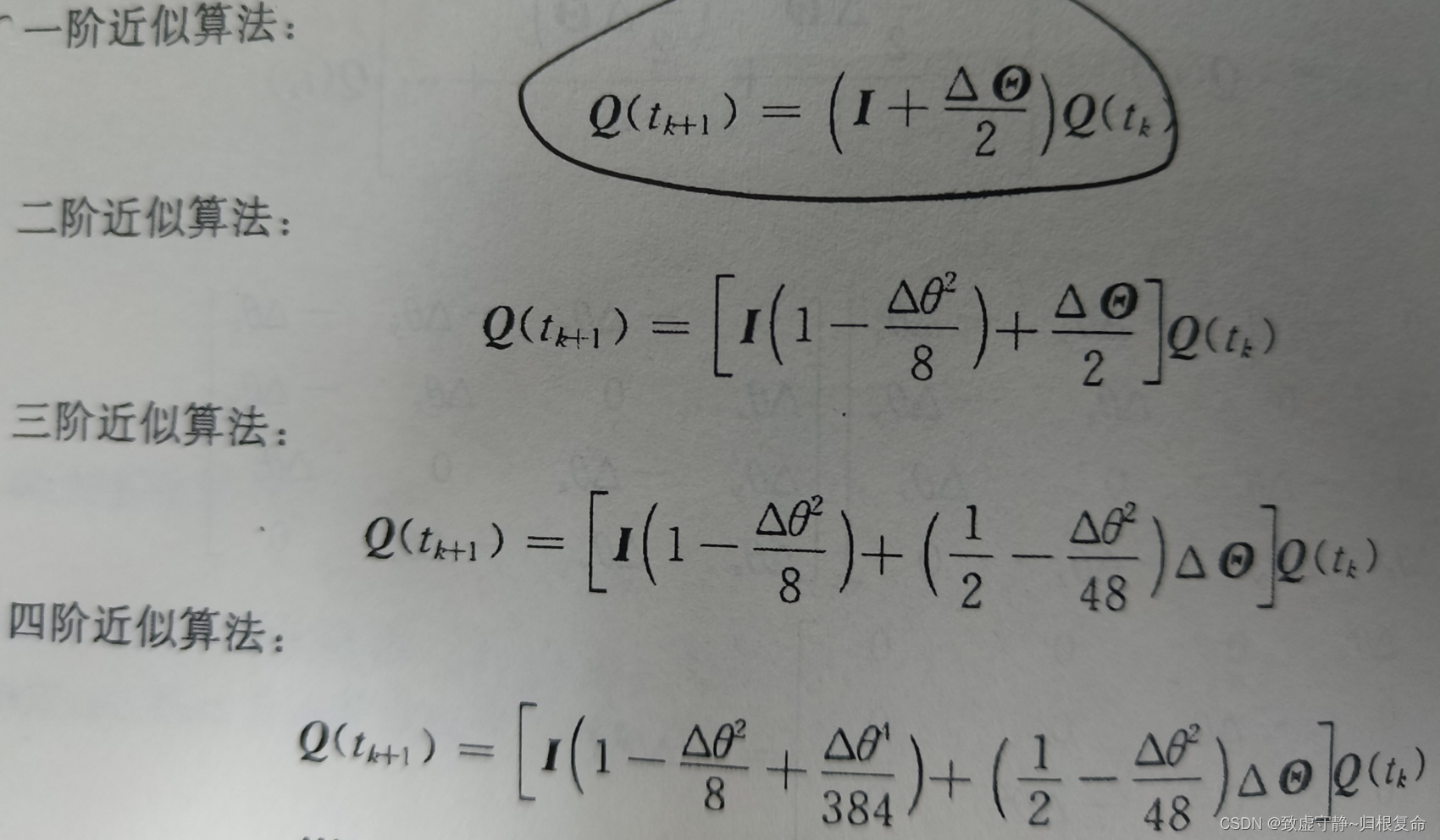
??一般通常使用一阶近似算法即可,四元数计算如下:
??当选取:
{
q
0
=
c
o
s
θ
2
q
1
=
l
s
i
n
θ
2
q
2
=
m
s
i
n
θ
2
q
3
=
n
s
i
n
θ
2
\begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases}
?
?
??q0?=cos2θ?q1?=lsin2θ?q2?=msin2θ?q3?=nsin2θ??
??
Q
(
k
+
1
)
Q(k+1)
Q(k+1)计算如下
Q
(
k
+
1
)
=
Q
(
k
)
+
1
2
(
0
?
Δ
θ
x
?
Δ
θ
y
?
Δ
θ
z
Δ
θ
x
0
Δ
θ
z
?
Δ
θ
y
Δ
θ
y
?
Δ
θ
z
0
Δ
θ
x
Δ
θ
z
Δ
θ
y
?
Δ
θ
x
0
)
Q
(
k
)
Q(k+1)= Q(k)+\frac{1}{2}\begin{pmatrix} 0&-\Delta\theta_x&-\Delta\theta_y&-\Delta\theta_z\\ \Delta\theta_x&0&\Delta\theta_z&-\Delta\theta_y\\ \Delta\theta_y&-\Delta\theta_z&0&\Delta\theta_x\\ \Delta\theta_z&\Delta\theta_y&-\Delta\theta_x&0\end{pmatrix}Q(k)
Q(k+1)=Q(k)+21?
?0Δθx?Δθy?Δθz???Δθx?0?Δθz?Δθy???Δθy?Δθz?0?Δθx???Δθz??Δθy?Δθx?0?
?Q(k)
?? 注意,在一些论文或者书籍中,
q
0
,
q
1
,
q
2
,
q
3
q_0,q_1,q_2,q_3
q0?,q1?,q2?,q3?与上面的选取不同,例如选取,当选取如下时:
{
q
0
=
l
s
i
n
θ
2
q
1
=
m
s
i
n
θ
2
q
2
=
n
s
i
n
θ
2
q
3
=
c
o
s
θ
2
\begin{cases}q_0=lsin\frac{\theta}{2}\\q_1=msin\frac{\theta}{2}\\q_2=nsin\frac{\theta}{2}\\q_3=cos\frac{\theta}{2}\end{cases}
?
?
??q0?=lsin2θ?q1?=msin2θ?q2?=nsin2θ?q3?=cos2θ??
??
Q
(
k
+
1
)
Q(k+1)
Q(k+1)计算如下
Q
(
k
+
1
)
=
Q
(
k
)
+
1
2
(
0
Δ
θ
z
?
Δ
θ
y
Δ
θ
x
?
Δ
θ
z
0
Δ
θ
x
Δ
θ
y
Δ
θ
y
?
Δ
θ
x
0
Δ
θ
z
?
Δ
θ
x
?
Δ
θ
y
?
Δ
θ
z
0
)
Q
(
k
)
Q(k+1)= Q(k)+\frac{1}{2}\begin{pmatrix} 0&\Delta\theta_z&-\Delta\theta_y&\Delta\theta_x \\ -\Delta\theta_z&0&\Delta\theta_x&\Delta\theta_y\\ \Delta\theta_y&-\Delta\theta_x&0&\Delta\theta_z\\ -\Delta\theta_x&-\Delta\theta_y&-\Delta\theta_z&0\end{pmatrix}Q(k)
Q(k+1)=Q(k)+21?
?0?Δθz?Δθy??Δθx??Δθz?0?Δθx??Δθy???Δθy?Δθx?0?Δθz??Δθx?Δθy?Δθz?0?
?Q(k)
五、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602
课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文
课题学习(十六)----阅读《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes Based…》论文
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!