DSGN：用于 3D 目标检测的深度立体几何网络

论文地址：https://www.jianshu.com/go-wild?ac=2&url=https%3A%2F%2Farxiv.org%2Fpdf%2F2001.03398v3.pdf
论文代码：https://github.com/chenyilun95/DSGN

论文背景

大多数最先进的 3D 物体检测器严重依赖 LiDAR 传感器，因为基于图像的方法和基于 LiDAR 的方法之间存在很大的性能差距。这是由在 3D 场景中形成预测表示的方式引起的。
3D 场景理解是 3D 感知中的一项具有挑战性的任务，它是自动驾驶和机器人技术的基本组成部分。由于 LiDAR 传感器准确检索 3D 信息的强大能力，人们提出了各种 3D 物体检测器来利用 LiDAR 点云表示。激光雷达的局限性在于多个激光束的数据分辨率相对稀疏，而且设备价格较高。
相比之下，摄像机更便宜并且分辨率更高。计算立体图像场景深度的方法是通过立体对应估计来考虑视差。尽管最近一些基于单目或立体设置的 3D 检测器突破了基于图像的 3D 物体检测的极限，但精度仍然远远落后与基于激光雷达的方法相比。

基于图像的方法面临的最大挑战之一是为预测 3D 目标提供适当且有效的表示。最近的工作将该任务分为两个子任务，即深度预测和目标检测。相机投影是将 3D 世界映射到 2D 图像的过程。不同物体姿态的一个 3D 特征会导致局部外观变化，使得 2D 网络很难提取稳定的 3D 信息。另一系列解决方案是生成中间点云，然后是基于 LiDAR 的 3D 目标检测器。这种 3D 表示效率较低，因为转换是不可微分的并且包含多个独立网络。此外，点云面临着 object artifacts 的挑战，这限制了后续 3D 目标检测器的检测精度。

论文框架

论文提出了一种基于立体的端到端 3D 对象检测 pipeline ——深度立体几何网络（Deep Stero Geometry Network，DSGN），它依赖于从 2D 特征到有效 3D 结构（称为 3D）的空间转换 geometric volume（3DGV）。
3DGV 在于构建编码 3D geometry 的 3D volume 的方法。 3D 几何 volume 在 3D 世界空间中定义，由相机平截头体中构造的平面扫描体 (plane-sweep volume，PSV) 转换而来。像素对应约束可以在 PSV 中很好地学习，而现实世界对象的 3D 特征可以在 3DGV 中学习。volume 构造是完全可微的，因此可以针对立体匹配和对象检测的学习进行联合优化。

这种 volume 表示有两个主要优点。首先，很容易施加像素对应约束并将完整深度信息编码到 3D 真实世界体积中。其次，它提供带有几何信息的 3D 表示，使学习现实世界对象的 3D 几何特征成为可能。

论文内容

动机

由于 perspective 的原因，物体随着距离的增加而显得更小，这可能使得根据目标大小和上下文的相对比例粗略地估计深度。然而，同一类别的 3D 目标仍可能具有不同的尺寸和方向，大大增加了准确预测的难度。
此外，透视缩短的视觉效果会导致图像中附近的 3D 目标缩放不均匀。普通的长方体汽车看起来像一个不规则的截头体。这两个问题给 2D 神经网络建模 2D 成像和真实 3D 目标之间的关系带来了重大挑战。
因此，通过反转投影过程，中间 3D 表示不依赖 2D 表示，而是为 3D 目标理解提供了一种更有前景的方法。

以下两种表示通常可以在 3D 世界中使用。
1.基于点的表示
当前最先进的 pipelines 通过深度预测方法生成点云的中间 3D 结构，并应用基于 LiDAR 的 3D 目标检测器。主要可能的弱点是它涉及多个独立网络，并且可能在中间转换过程中丢失信息，使得3D结构（例如成本量）归结为点云。这种表示经常会在物体边缘附近遇到条纹伪影。此外，网络对于多目标场景很难区分。
2.基于体素的表示
Volumetric representation 作为 3D 表示的另一种方式，研究较少。 OFT-Net_mono[1] 直接将图像特征映射到3D体素网格，然后将其折叠到鸟瞰图上的特征。但是，此转换保留了此视图的 2D 表示形式，并且没有显式编码数据的 3D 几何图形。

[1]Thomas Roddick, Alex Kendall, and Roberto Cipolla. Orthographic feature transform for monocular 3d object detection. 2019.

建立有效的 3D 表示的关键依赖于对 3D 空间的准确 3D 几何信息进行编码的能力。立体相机为计算深度提供了明确的像素对应约束。论文探索了能够提取立体对应的像素级特征和语义线索的高级特征的深层架构。另一方面，像素对应约束是沿着穿过每个像素的投影光线施加的，其中深度被认为是确定的。为此，论文从双目图像对创建中间平面扫描体，以学习相机平截头体中的立体对应约束，然后将其转换为 3D 空间中的 3D 体。在这个具有从平面扫描体积中提取的 3D 几何信息的 3D 体中能够很好地学习现实世界对象的 3D 特征。

Deep Stereo Geometry Network 深度立体几何网络

以双目图像对（$I_L$、$I_R$）的输入，论文通过 Siamese 网络提取特征并构建平面扫描体（PSV） 。像素对应关系是在该 volume 上学习的。通过可微扭曲，将 PSV 转换为 3D 几何体 (3DGV)，以在 3D 世界空间中建立 3D 几何。

图像特征提取

用于立体匹配和对象识别的网络针对各自的任务有不同的架构设计。为了保证立体匹配的合理精度，论文采用 PSMNet[2] 的主要设计。

Jia-Ren Chang and Yong-Sheng Chen. Pyramid stereo matching network. In CVPR, pages 5410–5418, 2018.

由于检测网络需要基于高级语义特征和大量上下文信息的判别性特征，因此修改网络以掌握更多高级信息。此外，用于成本量聚合的 3D CNN 需要更多的计算，这为论文提供了修改 2D 特征提取器的空间，从而无需在整个网络中引入额外的繁重计算开销。
2D 特征提取器的关键修改如下：
1.将更多计算量从 $con{v}_3$ 转移到 $con{v}_4$ 和 $con{v}_5$ ，即将 $con{v}_2$ 到 $con{v}_5$ 的 basic blocks 数量从 { 3 , 16 , 3 , 3 } \{3, 16, 3, 3\} {3,16,3,3} 更改为 { 3 , 6 , 12 , 4 } \{3, 6, 12, 4\} {3,6,12,4}。
2.PSMNet 中使用的 SPP 模块连接了 $con{v}_4$ 和 $con{v}_5$ 的输出层。
3.$con{v}_1$ 中卷积的输出通道数是 64 而不是 32，基本残差块的输出通道数是 192 而不是 128。

构建 3D 几何体

为了学习 3D 规则空间中的 3D 卷积特征，论文首先通过将平面扫描体扭曲??到 3D 规则空间来创建 3D 几何体积 (3DGV)。在不失一般性的情况下，将 3D 世界空间中的 ROI 区域沿着摄像机视图中的右、下和前方向离散化为尺寸为 $(W_V,H_V,D_V)$ 的 3D 体素占据网格。 $W_V,H_V,D_V$ 分别表示网格的宽度、高度和长度。每个体素的大小为 $(v_m,v_h,v_d)$。

平面扫描体 在双目视觉中，图像对 $(I_L,I_R)$ 用于构建基于视差的 cost volume 来计算匹配成本，该匹配成本将左图像 $I_L$中的像素 $i$ 与右图像 $I_R$ 中水平偏移了积分视差值 $d$ 的对应关系相匹配。深度与视差成反比。
由于相似的视差值，很难区分远处的物体。例如，40 米和 39 米外的物体在 KITTI 基准上的视差几乎没有差异（< 0.25pix）。
以不同的方式构建 cost volume，遵循经典的平面扫描方法，通过以等间隔的深度间隔来连接左图像特征 $F_L$ 和重新投影的右图像特征 $F_{R\to L}$ 来构建平面扫描体，避免特征到 3D 空间的不平衡映射。
PSV 的坐标由 $(u,v,d)$ 表示，其中 $(u,v)$ 表示图像中的 $(u,v)$ 像素，并且它添加了另一个与图像平面正交的轴以表示深度。将$(u,v,d)$ 空间称为 camera frustum 空间。深度候选 $d_i$ 沿着深度维度以间隔 $v_d$ 遵循预定义的 3D 网格进行均匀采样。基于串联的 volume 使网络能够学习目标识别的语义特征。
对这个 Volume 应用 3D 卷积，最终得到所有深度的匹配 cost volume。为了简化计算，与 PSMNet 中使用的三个 hourglass 模块相比，仅应用一个 3D hourglass 模块。由于整个网络是可微的，因此所产生的性能下降可以在以下检测网络中得到补偿。

3D几何体 在已知相机内部参数的情况下，通过反转 3D 投影将 PSV 在计算匹配成本之前的最后一个特征图从 camera frustum 空间 $(u,v,d)$ 转换为3D世界空间 $(x,y,z)$：
$$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{ccc}1/f_x& 0& ?c_u/f_x\\ 0& 1/f_y& ?c_v/f_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}ud\\ vd\\ d\end{array}\right)$$

其中 $f_x$、$f_y$ 是水平和垂直焦距。这种变换是完全可微的，并且通过消除预定义网格之外的背景（例如天空）来节省计算量。它可以通过三线性插值的扭曲操作来实现。

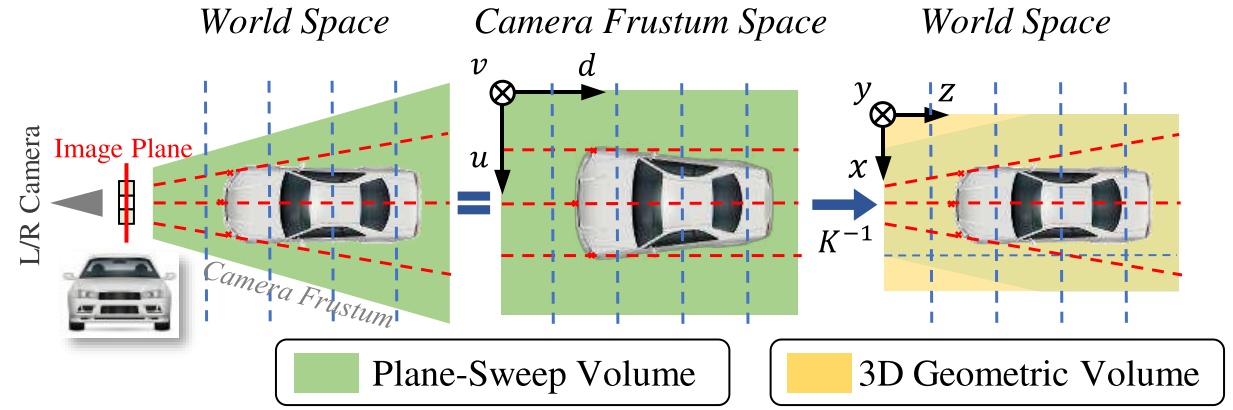
上图说明了转换过程。常见的像素对应约束（红色虚线）施加在 camera frustum 体中，而目标识别是在常规 3D 世界空间（欧几里得空间）中学习的。这两种表述显然存在差异。
图像是在图像平面（红色实线）处捕获的。PSV 通过在左相机视锥体中以等距深度（蓝色虚线）投影图像来构建，这在 3D 世界空间（左）和相机视锥体空间（中）中显示。显示汽车在中间扭曲。通过相机内在矩阵 K 进行映射，PSV 被扭曲为 3DGV，从而恢复了汽车。

在平面扫描体的最后一个特征图中，低成本体素 $(u,v,d)$ 意味着沿通过焦点和图像点 $(u,v)$ 的射线存在于深度 $d$ 处的物体的高概率。随着向常规3D世界空间的变换，低成本的特征表明该体素占据场景的前表面，可以作为3D几何结构的特征。因此，以下 3D 网络可以学习该卷上的 3D 对象特征。
该操作与可微分非投影有着根本的不同，可微分非投影通过双线性插值直接将图像特征从2D图像帧提升到3D世界。论文的目标是将几何信息从 cost volume 提升到 3D 世界网格。使像素对应约束很容易沿着投影光线施加。
像平面扫描体一样构造 depth-cost-volume 。不同的是，论文的目标是避免从平面扫描体到 3D 几何体的不平衡扭曲，并处理 streaking artifact 问题。此外，变换保留了深度的分布，而不是将其推导出深度图。论文的策略避免了 object artifacts。

平面扫描 cost volume 的深度回归

为了计算平面扫描体上的匹配成本，论文通过两个 3D 卷积减少平面扫描体的最终特征图，以获得 1D cost volume（称为平面扫描 planes-weep cost volume）。
Soft arg-min 运算用于计算所有深度候选的期望，概率为 $\sigma (?c_d)$： d ^ = ∑ d ∈ { z min ? , z min ? + v d , . . . , z max ? } d × σ ( ? c d ) \hat d = \sum_{d \in \{ z_{\min},z_{\min}+v_d,...,z_{\max} \}} d \times \sigma(-c_d) d^=d∈{zmin?,zmin?+vd?,...,zmax?}∑?d×σ(?cd?)

其中深度候选在预定义网格 $[z_{\min },z_{\max }]$ 内以间隔 $v_d$ 均匀采样。 softmax 函数使得模型为每个像素选择一个深度平面。

3D 几何体上的 3D 目标检测器

受最近的单级 2D 探测器 FCOS 的推动，我们在 pipeline 中扩展了中心分支的想法，并设计了一种基于距离的策略来为现实世界分配目标。由于 3D 场景中同一类别的目标大小相似，所以仍然保留 anchor 的设计。

令 $\mathcal{V}\in {\mathbb{R}}^{\mathcal{W}\times \mathcal{H}\times \mathcal{D}\times \mathcal{C}}$ 为尺寸为 $(W,H,D)$ 的 3DGV 的特征图，并将通道表示为 $C$。考虑到自动驾驶的场景，我们沿着高度维度逐渐下采样，最终得到用于鸟瞰图的尺寸为 $(W,H)$ 的特征图 $\mathcal{F}$。

对于 $\mathcal{F}$ 中的每个位置 $(x,z)$，放置几个不同方向和大小的锚点。锚点 $A$ 和真实框 $G$ 由位置、先验大小和方向表示，即 $(x_A,y_A,z_A,h_A,w_A,l_A,{\theta }_A)$ 和 $(x_G,y_G,z_G,h_G,w_G,l_G,{\theta }_G)$。从锚点回归并得到最终的预测 $(h_A{e}^{\delta h},w_A{e}^{\delta w},l_A{e}^{\delta l},x_A+\delta x,y_A+\delta y,z_A+\delta z,{\theta }_A+\pi /N_{\theta }\tanh (\delta \theta ))$，其中 $N_{\theta }$ 表示的是锚点方向的数量，$\delta$ 是每个参数的可学习偏差。

基于距离的目标分配 考虑到面向目标，论文提出基于距离的目标分配。该距离定义为锚点和真实框之间 8 个角的距离：
$$distance(A,G)=\frac{1}{8}\sum _{i=1}^8\sqrt{(x_{A_i}?x_{G_i}{)}^2+(z_{A_i}?z_{G_i}{)}^2}$$

为了平衡正负样本的比例，论文让前 $N$ 个与 ground-truth 距离最近的 anchor 作为正样本，其中 KaTeX parse error: Undefined control sequence: \× at position 7: N = γ \?×? k，$k$ 是鸟瞰图上 ground-truth 框内的体素数量。$\gamma$ 调整正样本的数量。中心度定义为八个角的负归一化距离的指数：$$centerness(A,G)=e^{?\text{norm}(distance(A,G))}$$ 其中 norm 表示 min-max 归一化。

多任务训练

网络具有立体匹配网络和 3D 目标检测器，以端到端的方式进行训练。用多任务损失训练整体 3D 物体检测器：$$Loss={\mathcal{L}}_{depth}+{\mathcal{L}}_{cls}+{\mathcal{L}}_{reg}+{\mathcal{L}}_{centerness}$$

对于深度回归的损失，在该分支中采用平滑的 L1 损失：$${\mathcal{L}}_{depth}=\frac{1}{N_D}\sum _{i=1}^{N_D}smoot{h}_{L_1}(d_i?{\hat{d}}_i)$$

其中 $N_D$ 是具有地面真实深度的像素数（从稀疏 LiDAR 传感器获得）。

对于分类损失，网络采用焦点损失来处理 3D 世界中的类不平衡问题：$${\mathcal{L}}_{cls}=\frac{1}{N_{pos}}\sum _{(x,z)\in \mathcal{F}}Foca{l}_{L}oss(p_{A_{(x,z)}},p_{G_{(x,z)}})$$

其中 $N_{pos}$表示正样本的数量。Binary cross-entropy 交叉熵（BCE）损失用于中心度。
对于 3D 边界框回归的损失，使用 smooth $L_1$ Loss 进行边界框的回归，如下所示：
$${\mathcal{L}}_{reg}=\frac{1}{N_{pos}}\sum _{(x,z)\in F_{pos}}\text{centerness}(A,G)\times {\text{smooth}}_{L_1}(l1\_distance(A,G))$$

其中 $F_{pos}$ 表示鸟瞰图上的所有正样本。

在联合学习和不联合学习所有参数的情况下尝试两个不同的回归目标。
1.单独优化框参数。回归损失直接应用于 $(x,y,z,h,w,l,\theta )$ 的偏移量。
2.共同优化框角点。为了联合优化框参数，根据 3D 锚点预测框和真实框之间八个框角的平均 L1 距离进行损失。

论文贡献

1.为了弥合 2D 图像和 3D 空间之间的差距，在平面扫描体中建立 stereo correspondence，然后将其转换为 3D 几何体积，以便能够对 3D 几何和语义线索进行编码，以便在 3D 规则空间中进行预测。
2.设计了一个端到端的 pipeline，用于提取用于立体匹配的像素级特征和用于对象识别的高级特征。所提出的网络联合估计场景深度并检测 3D 世界中的 3D 目标，从而实现许多实际应用。

论文总结

论文在双目图像上提出了一种新的 3D 目标检测器。它表明基于端到端立体的 3D 物体检测是可行且有效的。统一网络通过将平面扫描体转换为 3D 几何体积来对 3D 几何体进行编码。因此，它能够学习 3D 体上 3D 对象的高质量几何结构特征。联合训练让网络学习像素和高级特征，以完成立体匹配和 3D 目标检测的重要任务。