数据结构篇-顺序表及单项链表
目录
一、学习目标
- 知识点:
- 一文掌握数据结构的顺序表和单项链表
- 通过打怪实战来提升自己的理解
二、顺序表
1. 线性表
????????1.1 概念
????????对于一组拥有n个数据元素的线性表,其严格数学定义是:其中任何一个数据元素ai,有且仅有一个直接前驱ai-1,有且仅有一个直接后继ai+1,首元素a0无直接前驱, 尾元素an-1无直接后继。
????????满足这种数学关系的一组数据,当中的数据是一个挨着一个的,常被称为一对一关系。反之,如果数据之间的关系不是一对一的,就是非线性的。
????????1.2 举例
????????生活中的线性表例子非常多,比如一个班级中的以学号编排的学生,一座图书馆中的以序号编排的图书、一条正常排队等候的队列、一摞从上到下堆叠的餐盘,这些都是线性表。他们的特点都是:除了首尾两个元素,其余任何一个元素前后都对应相邻的另一个元素。

注意:线性表是一种数据内部的逻辑关系,与存储形式无关线性表既可以采用连续的顺序存储,也可以采用离散的链式存储
2. 顺序表
????????2.1 基本概念
- 顺序表:顺序存储的线性表。
- 链式表:链式存储的线性表,简称链表。
????????顺序存储就是将数据存储到一片连续的内存中,在C语言环境下,可以是具名的栈数组,或者是匿名的堆数组。
????????存储方式不仅仅只是提供数据的存储空间,而是必须要能体现数据之间的逻辑关系。当采用顺序存储的方式来存放数据时,唯一能用来表达数据间本身的逻辑关系的就是存储位置。比如队列中的两个人,小明和小花,如果小明在逻辑上排在相邻的小花的前面,那么在存储位置上也必须把小明存放在相邻的小花的前面。

????????2.2 基本操作
- 顺序表设计(顺序表的管理结构体)
-
- 顺序表总容量
- 顺序表当前最末元素下标位置
- 顺序表入口指针
typedef int DataType ;
// 设计一个顺序表的管理结构体
typedef struct list
{
int Capacity; // 顺序表总容量
int End; // 末尾数据下标
DataType * Entrance ; // 顺序表的入口地址
} List , *P_List ;- 初始化

P_List ListInit( unsigned int Size )
{
// 申请一个管理结构体的空间
P_List Cntl = calloc( 1 , sizeof(List) );
if (Cntl == NULL)
{
perror("calloc Cntl error");
return NULL ;
}
// 申请数据的存储空间,并把申请到的内存入口地址填入到管理结构体中
Cntl->Entrance = calloc( Size , sizeof(DataType) );
if (Cntl->Entrance == NULL)
{
perror("calloc Data error");
free(Cntl); // 释放管理结构体
return NULL ;
}
Cntl->End = -1 ; // 初始化管理结构体中的末尾元素下标
Cntl->Capacity = Size; // 初始化管理结构体中总容量
// 返回管理结构体地址
return Cntl ;
}- 添加数据
bool Add2List( P_List Cntl , DataType NewData )
{
// 判断顺序表是否已满
if (Cntl->End == Cntl->Capacity - 1 )
{
printf("当前顺序表已满...\n");
return false ;
}
// 比较并找到合适的位置进行插入
int i = 0 ;
for ( i = 0; i <= Cntl->End; i++)
{
if ( Cntl->Entrance[i] > NewData )
{
// 从当前的i的位置开始把右边的所有的数据以此(从右往左)右移
Move2Right( Cntl , i );
break;
}
}
// 插入
// Cntl->Entrance[i] = NewData ;
memcpy( Cntl->Entrance+i , &NewData , sizeof(DataType) );
// 更新末尾数据下标
Cntl->End ++ ;
return true ;
}- 遍历显示数据
void DisplayList( P_List Cntl )
{
// 判断当前顺序表是否为空
if (Cntl->End < 0)
{
printf("当前顺序表为空...\n");
return ;
}
for (int i = 0; i <= Cntl->End ; i++)
{
printf("%d\n" , Cntl->Entrance[i]);
}
return ;
}- 查找数据
int FindData( P_List Cntl , DataType Data )
{
// 判断当前顺序表是否为空
if (Cntl->End < 0)
{
printf("当前顺序表为空...\n");
return -1 ;
}
for (int i = 0; i <= Cntl->End ; i++)
{
if (Cntl->Entrance[i] == Data)
{
printf("成功找到指定的数据,他的存储位置是:%d\n" , i );
return i ;
}
}
printf("无法找到指定的数据....\n");
return -1 ;
} - 删除数据
DataType Del4List ( P_List Cntl , unsigned int Index )
{
if ( Cntl->End < Index)
{
printf("接收到错误的参数下标..\n");
return -1 ;
}
DataType tmp = Cntl->Entrance[Index];
// 从左往右依次左移操作
MoveLeft( Cntl , Index );
Cntl->End -- ;
return tmp ;
}- 修改数据
void UpData(P_List Cntl , DataType Data )
{
// 找到目数据
int Index = FindData(Cntl , Data );
if (Index < 0)
{
printf("修改数据失败...\n");
return ;
}
// 剔除该数据
Del4List( Cntl , Index );
// 获取新的数据
DataType NewData = GetNewData( );
// 有序插入
Add2List(Cntl , NewData );
}2.3 顺序表优缺点总结
????????顺序存储中,由于逻辑关系是用物理位置来表达的,因此从上述示例代码可以很清楚看到,增删数据都非常困难,需要成片地移动数据。顺序表对数据节点的增删操作是很不友好的。
总结其特点如下:
- 优点
- 不需要多余的信息来记录数据间的关系,存储密度高
- 所有数据顺序存储在一片连续的内存中,支持立即访问任意一个随机数据(立即访问),比如上述顺序表中第 i 就可以直接 Cntl->Ent[i] .
- 缺点
- 插入、删除时需要保持数据的物理位置反映其逻辑关系,一般需要成片移动数据
- 当数据节点数量较多时,需要一整片较大的连续内存空间
- 当数据节点数量变化剧烈时,内存的释放和分配不灵活
三、单项链表
1. 基本概念
- 顺序表:顺序存储的线性表。
- 链式表:链式存储的线性表,简称链表。
????????既然顺序存储中的数据因为挤在一起而导致需要成片移动,那很容易想到的解决方案是将数据离散地存储在不同内存块中,然后在用来指针将它们根据数据的逻辑关系串起来。这种朴素的思路所形成的链式线性表,就是所谓的链表。
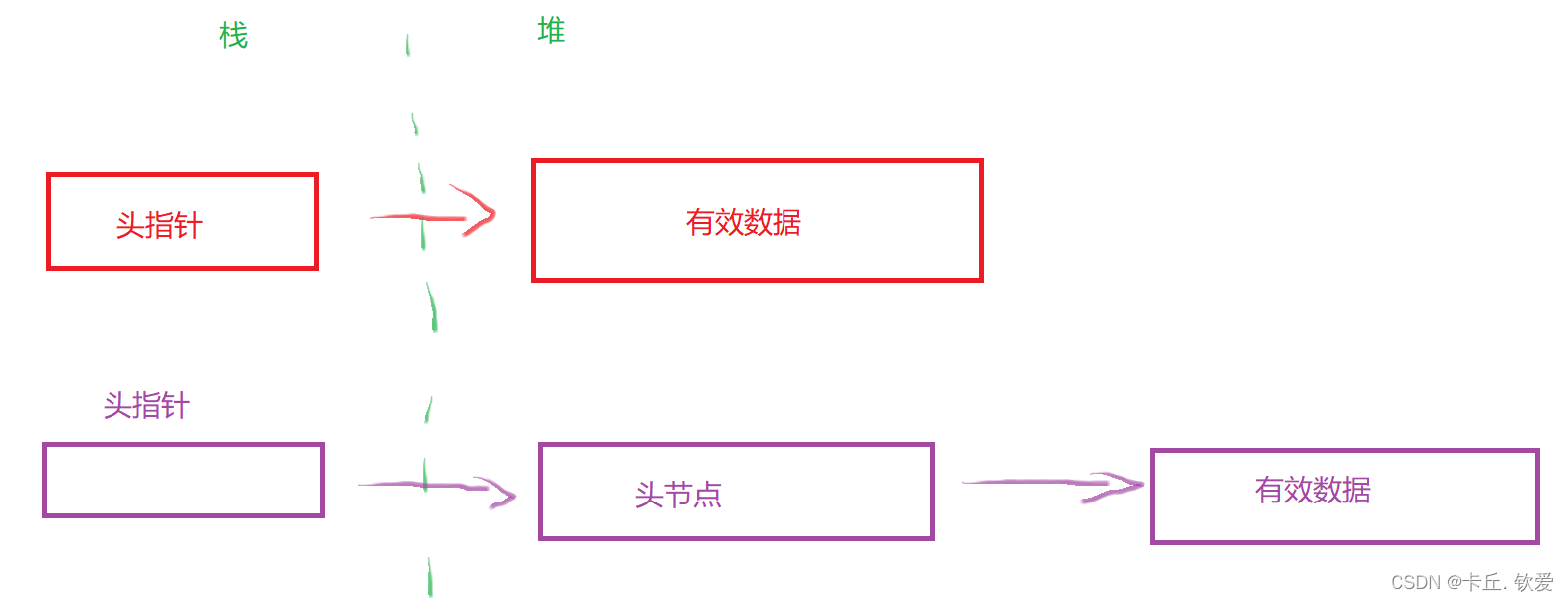
顺序表和链表在内存在的基本样态如下图所示:
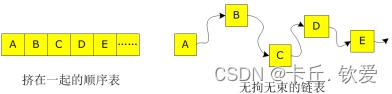
2. 链表的分类
根据链表中各个节点之间使用指针的个数,以及首尾节点是否相连,可以将链表细分为如下种类:
- 单向链表 (每一个节点只有一个指针,指向下一个数据的地址)
- 单向循环链表 (尾部节点的下一个指针指向的是头部节点)
- 双向循环链表 (每一个节点都有两个指针, 它分别指向上一个以及下一个接下,并首尾节点互相指向)
- 内核链表 (本质上是一个双向循环链表,与其他链表不同之处就在于的数据与链表的逻辑是剥离的)
这些不同链表的操作都是差不多的,只是指针数目的异同。以最简单的单向链表为例,其基本示意图如下所示:
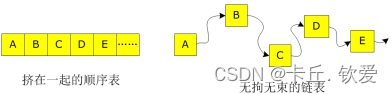
????????上图中,所有的节点均保存一个指针,指向其逻辑上相邻的下一个节点(末尾节点指向空)。另外注意到,整条链表用一个所谓的头指针 head 来指向,由 head 开始可以找到链表中的任意一个节点。head 通常被称为头指针。
链表的基本操作,一般包括:
- 节点设计
- 初始化空链表
- 增删节点
- 链表遍历
- 销毁链表
下面着重针对这几项常见操作,讲解单向链表的处理。
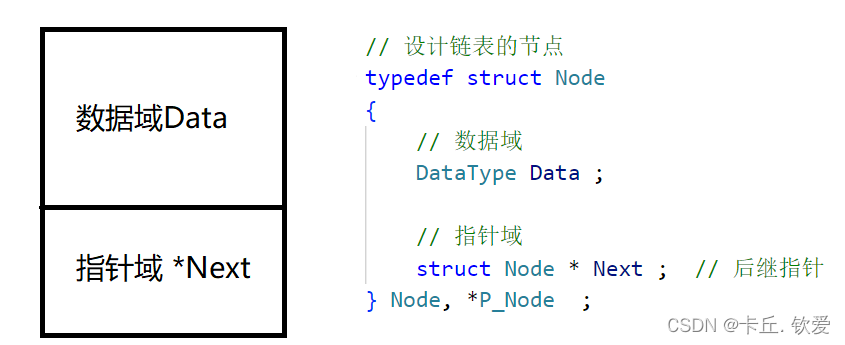
- 节点设计
- 初始化空链表
无头节点:
概念: 链表的头部没有多余的一个节点,所有的节点都用于存储有效数据。

P_Node head = NULL ;有头节点:
概念: 链表的头部有一个多余的节点,该节点不存储有效数据,作用是可以防止链表在操作的时候丢失的问题。

P_Node InitList( void )
{
// 申请头节点
P_Node head = calloc( 1, sizeof(Node) );
if (head == NULL)
{
perror ( "calloc head error" );
return NULL ;
}
// 初始化头节点的指针域指向空
head->Next = NULL ;
// 返回给头节点
return head;
}-
增添加节点
头插法:

void Add2Head( P_Node head , P_Node New )
{
// 1. 让新新节点的后继指针指向第一个有效数据 head->Next
New->Next = head->Next ;
// 2. 让头节点的后继指针指向新节点
head->Next = New ;
return ;
}尾补插入:
void Add2Tail( P_Node head , P_Node New )
{
P_Node tmp ;
// 使用临时指针tmp 找到链表的最后一个有效的数据节点
for ( tmp = head ; tmp->Next != NULL; tmp = tmp->Next);
// 从for 循环出来后 tmp 就指向了最后一个节点
// 1. 更新新节点的后继指针
New->Next = tmp->Next ;
// 2. 更新末尾节点的后继指针
tmp->Next = New ;
return ;
}任意位置插入(插入到某一个节点的后方):
void Add2List ( P_Node Prev , P_Node New )
{
New->Next = Prev->Next ;
Prev->Next = New ;
return ;
}有序插入:
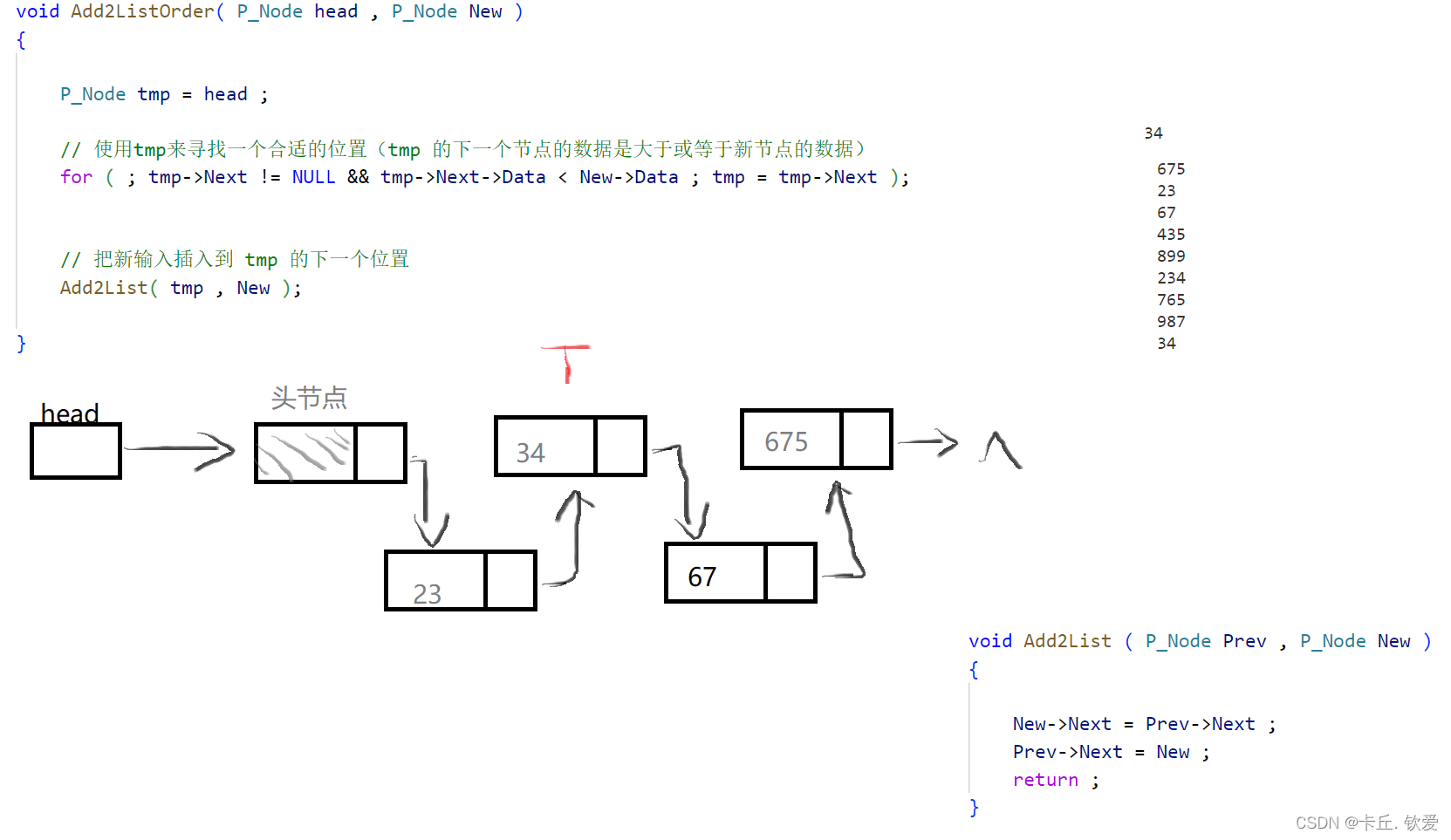
代码:
void Add2ListOrder( P_Node head , P_Node New )
{
P_Node tmp = head ;
// 使用tmp来寻找一个合适的位置(tmp 的下一个节点的数据是大于或等于新节点的数据)
for ( ; tmp->Next != NULL && tmp->Next->Data < New->Data ; tmp = tmp->Next );
// 把新输入插入到 tmp 的下一个位置
Add2List( tmp , New );
}遍历显示
void DisplayList( P_Node head )
{
for (P_Node tmp = head->Next ; tmp != NULL ; tmp = tmp->Next)
{
printf("数据:%d\n" , tmp->Data);
}
return ;
}-
查找节点
????????注意: 在单向链表的操作中一般需要得到目标操作节点的前驱节点,但是由于单向没有前驱指针,所以查找函数返回的是目标节点的前一个节点的指针。
P_Node FindNode ( P_Node head , DataType DelData )
{
P_Node tmp = NULL ;
// 使用for寻找需要剔除的节点
for ( tmp = head ; tmp->Next != NULL && tmp->Next->Data != DelData; tmp = tmp->Next);
// 如果没有找到指定数据
if (tmp->Next==NULL)
{
return NULL ;
}
return tmp ;
}-
删除节点
P_Node Del4List( P_Node head , DataType DelData )
{
// 链表是否为空
if (head->Next == NULL)
{
printf("链表为空。。。\n" );
return NULL ;
}
// 在链表中寻找需要删除的节点的前驱节点
P_Node Prev = FindNode ( head , DelData );
if (Prev == NULL)
{
printf("找不到需要剔除的节点...\n");
return NULL ;
}
printf("找到目标节点:%d\n" , Prev->Next->Data );
P_Node del = Prev->Next ;
// 剔除操作
Prev->Next = del->Next ;
del->Next = NULL ;
// 返回被剔除的节点
return del ;
}-
链表遍历
void DisplayList( P_Node head )
{
for (P_Node tmp = head->Next ; tmp != NULL ; tmp = tmp->Next)
{
printf("数据:%d\n" , tmp->Data);
}
return ;
}-
销毁链表
void DestroyLisr(P_Node head )
{
// 直接退出的条件
if (head == NULL)
{
return ;
}
DestroyLisr(head->Next);
free(head);
return ;
}有头节点与无头节点的关系:
????????无头节点的链表在操作时需要时刻关系栈中的 头指针 的指向,在插入或删除第一个数据时会改变头指针的指向。
????????有头节点的链表在操作时不需要关注 头指针 的指向,因为在做任何操作都不会改变头指针与头节点的关系,头指针永远指向头节点。也就是说栈中的头指针的值是永远不需要改变的。

拓展方向:
-
- 理解以上所写的基础版本代码
- 初始化函数和创建新节点函数如何融合。
- 头插尾插
- 有序插入
- 通用性
单向循环链表:
????????概念: 该链表的末尾节点的后继指针指向头节点。
????????与非循环链表的不同之处在于如何判断链表的末尾:
//非循环链表:
tmp->Next == NULL ; // tmp 则指向的末尾节点
//循环链表:
tmp->Next = head ; // tmp 指向的是末尾节点
打怪实战:
-
-
- 按照自己的能力手搓链表
- 链表的基础增删改查销毁
- 有序插入
- 【拓展】循环链表
- 【拓展】假设两个链表各自有序,请设计一个函数把这两个链表进行合并后返回
- 按照自己的能力手搓链表
-
????????????????????????????????L1 : 1 4 5 7 9 L2 : 3 6 7 8 10 合并后: L2 : 1 3 4 5 6 7 7 8 10
-
-
- 【拓展】假设有两个链表请设计一个函数把这两个链表进行合并
-
????????????????????????????????L1 : 1 4 5 7 9 L2 : 3 6 7 8 10 合并后: L2 : 3 6 7 8 10 1 4 5 7 9
四、总结
? ? ? ? 本文介绍了数据结构的顺序表和单项链表的基础概念和操作,理解本文所有知识点后,便可打败其中的小怪,拿下经验值~
? ? ? ? 本文参照?粤嵌文哥?部分课件经整理和修改后发布在C站,如有转载,请联系本人
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!