基于梯度和频率域的深度超分辨率新方法笔记二
一、实现方法和网络结构的剖析
1.1 网络结构
梯度校准模块(GCM)和频率感知模块(FAM)
1)梯度校准模块(GCM)
1、使用梯度映射函数(如下图所示),将RGB和LR深度图映射到梯度域
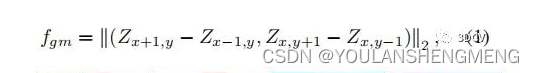
2、再梯度域中使用RGB的梯度特性对LR的梯度特征进行校准和锐化。这个过程是基于深度学习的,主要使用梯度感知损失进行有监督的学习。
3、将校准后的梯度特征和深度特征融合得到梯度增强后的特征,然后将梯度增强后的特征送入到频域感知模块。
2)频率感知模块(FAM)
? ? ? FAM如图3绿色区域所示,其递归的执行多个频谱差分模块来不断地在频域中优化深度特征。然后将不同阶段获取到的深度特征通过残差模块和上采样模块进行融合得到 ,最后结合由bicubic插值上采样后的深度图??, 得到最终预测的HR深度图??。
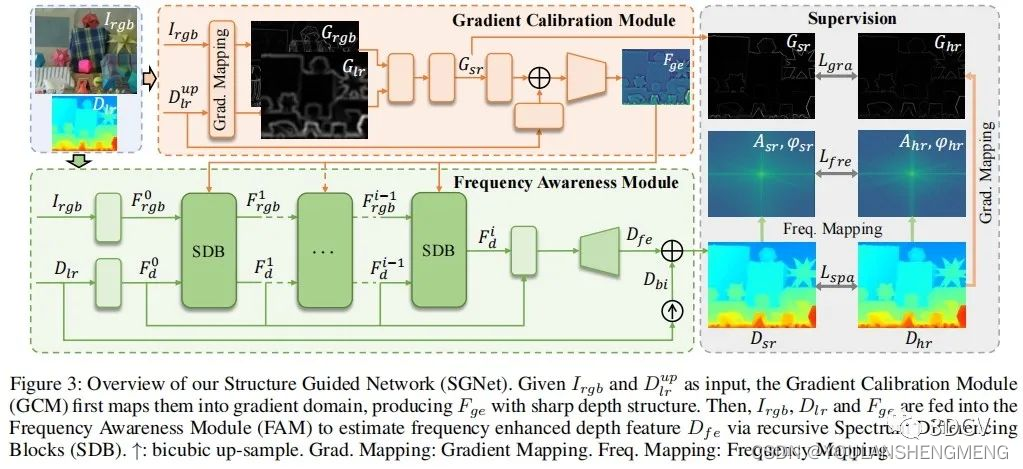
执行流程为:
1、递归的执行多个频谱差分模块来不断地在频域中优化深度特征
2、将不同阶段获取到的深度特征通过残差模块和上采样模块进行融合得到 Dfe.
3、最后结合由bicubic插值上采样后的深度图 Dbi, 得到最终预测的HR深度图??。

频谱差分模块:
由此可以得出:在频域中,是通过卷积层对幅值和相位的学习


频谱的相位和幅值的求解方法:
??快速傅里叶变换(FFT)是信号处理的重要组成部分,用于求信号的幅度、相位以及画频谱图等。
function [x,freq] = fft_plot(x,Fs)
%计算信号的双边幅度频谱和其横坐标、并调整使得横坐标中心频率为0Hz,输入:x为输入信号,Fs为采样频率,输出:x为输入信号的幅度频谱,freq为输入信号幅度频谱的横坐标
N = length(x);
%%计算频谱的横坐标,使得中心频率为0Hz
if mod(N,2)==0
k = -N/2:N/2-1;
else
k = -(N-1)/2:(N-1)/2;
end
T = N/Fs;
freq = k/T;
x= fft(x)/N;%fft并归一化
x= fftshift(x);
主程序:
[x1,freq] = fft_plot(x,Fs);
figure;
plot(freq,abs(x1));
xlabel('频率(Hz)');
ylabel('幅度');
title('信号频谱图');
?信号的频域表示携带每个频率下信号幅值和相位的有关信息。因此,FFT 计算的输出是复数。复
?有实部?
![]()
?和虚部?
![]()
,满足?
![]()
?的幅值计算为?
![]()
?的相位计算为?
![]()
3)损失函数

?二、损失函数
2.1 损失函数的作用
一:什么是损失函数:
简单的理解就是每一个样本经过模型后会得到一个预测值,然后得到的预测值和真实值的差值就成为损失(当然损失值越小证明模型越是成功),我们知道有许多不同种类的损失函数,这些函数本质上就是计算预测值和真实值的差距的一类型函数,然后经过库(如pytorch,tensorflow等)的封装形成了有具体名字的函数。
二:为什么需要损失函数:
我们上文说到损失函数是计算预测值和真实值的一类函数,而在机器学习中,我们想让预测值无限接近于真实值,所以需要将差值降到最低(在这个过程中就需要引入损失函数)。而在此过程中损失函数的选择是十分关键的,在具体的项目中,有些损失函数计算的差值梯度下降的快,而有些下降的慢,所以选择合适的损失函数也是十分关键的。
三:损失函数通常使用的位置:
在机器学习中,我们知道输入的feature(或称为x)需要通过模型(model)预测出y,此过程称为向前传播(forward pass),而要将预测与真实值的差值减小需要更新模型中的参数,这个过程称为向后传播(backward pass),其中我们损失函数(lossfunction)就基于这两种传播之间,起到一种有点像承上启下的作用,承上指:接収模型的预测值,启下指:计算预测值和真实值的差值,为下面反向传播提供输入数据。
2.2 常用的损失函数

代码实现:?
import torch as th
import torch.nn as nn
loss=nn.L1Loss()
input=th.Tensor([2,3,4,5])
target=th.Tensor([4,5,6,7])
output=loss(input,target)
output
tensor(2.)
我们可以用手动计算来验证数学本质正不正确(数学本质中的m在文中具体数值为4):
output=(|2-4|+|3-5|+|4-6|+|5-7|)/4=2
ps:因为我们函数的“reduction”(l1loss函数的参数)选择的是默认的"mean"(平均值),所以还会在除以一个"4",如果我们设置“loss=L1Loss(reduction='sum')则不用再除以4。
2,MSELoss函数:
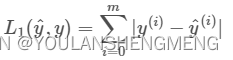
?ps:在此数学公式中的参数含义与L1Loss函数参数意义相同
import torch as th
import torch.nn as nn
loss=nn.MSELoss()
input=th.Tensor([2,3,4,5])
target=th.Tensor([4,5,6,7])
output=loss(input,target)
output
tensor(4.)
output=[(2-4)^2+(3-5)^2+(4-6)^2+(5-7)^2? ]/4=4
3:CrossEntropyLoss函数(交叉熵函数)

import torch
import torch.nn as nn
import math
loss = nn.CrossEntropyLoss()
input = torch.randn(1, 5, requires_grad= True)
target = torch.empty(1, dtype = torch.long).random_(5)
output = loss(input, target)
print('输入为5类:', input)
print('要计算loss的真实类别', target)
print('loss=', output)
#自己计算的结果
first = 0
for i in range(1):
first -= input[i][target[i]]
second = 0
for i in range(1):
for j in range(5):
second += math.exp(input[i][j])
res = 0
res += first + math.log(second)
print('自己的计算结果:', res)
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!