leetcode面试经典150题——36 旋转图像

题目： 旋转图像

描述：
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1：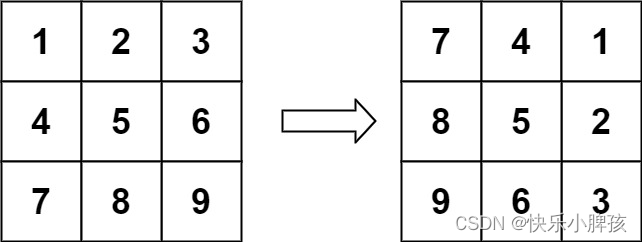
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
leetcode链接

方法一：(使用额外数组)
我们通过把矩阵顺时针旋转90度，可以发现， 第一行的元素到了倒数第一列，第二行的元素到了倒数第二列，以此类推，第i行的元素，变到了n-i-1(i从0开始)列，相同的第一列的元素变到了第一行，…第j列的元素变到了第j行，因此对于i行j列的元素，旋转后的位置应该为第j行n-i-1列，因此我们定义一个相同大小的矩阵，遍历原矩阵的每个元素，存储至新矩阵旋转后的位置上。
由于原题要求原地旋转图像，则不能申请新的内存空间，所以此方法不可行
时间复杂度：o(n2)
空间复杂度：o(n2)

void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        auto new_matrix = matrix;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                //i行j列元素变到j行n-i-1列
                new_matrix[j][n-i-1] = matrix[i][j];
            }
        }
        matrix = new_matrix;
    }

方法二：找规律
由方法一可知：对于matrix[i][j]，旋转后的新位置为matrix[j][n-i-1]，matrix[j][n-i-1]旋转后的位置为matrix[n-i-1][n-j-1],matrix[n-i-1][n-j-1]旋转后的位置为matrix[n-j-1][i],matrix[n-j-1][i]旋转后的位置为matrix[i][j],此时我们惊讶的发现对于一个元素旋转四次后会恢复到原点，很好理解，一个n阶矩阵每次旋转90度，旋转360度后会回到原位置。
知道上述规律后，我们不再定义一个新的矩阵，而是定义一个temp变量，记录最开始的matrix[i][j],而最后第四个元素旋转后的元素就应该是temp。现在我们把一个矩阵平分为4块，当n为奇数时中间剩一块，中间剩下的那一块旋转后不变。因此我们只需要对其中任意一块，对它进行旋转4次，即可得到答案。如下图所示
时间复杂度：o(n2)
空间复杂度：o(1)

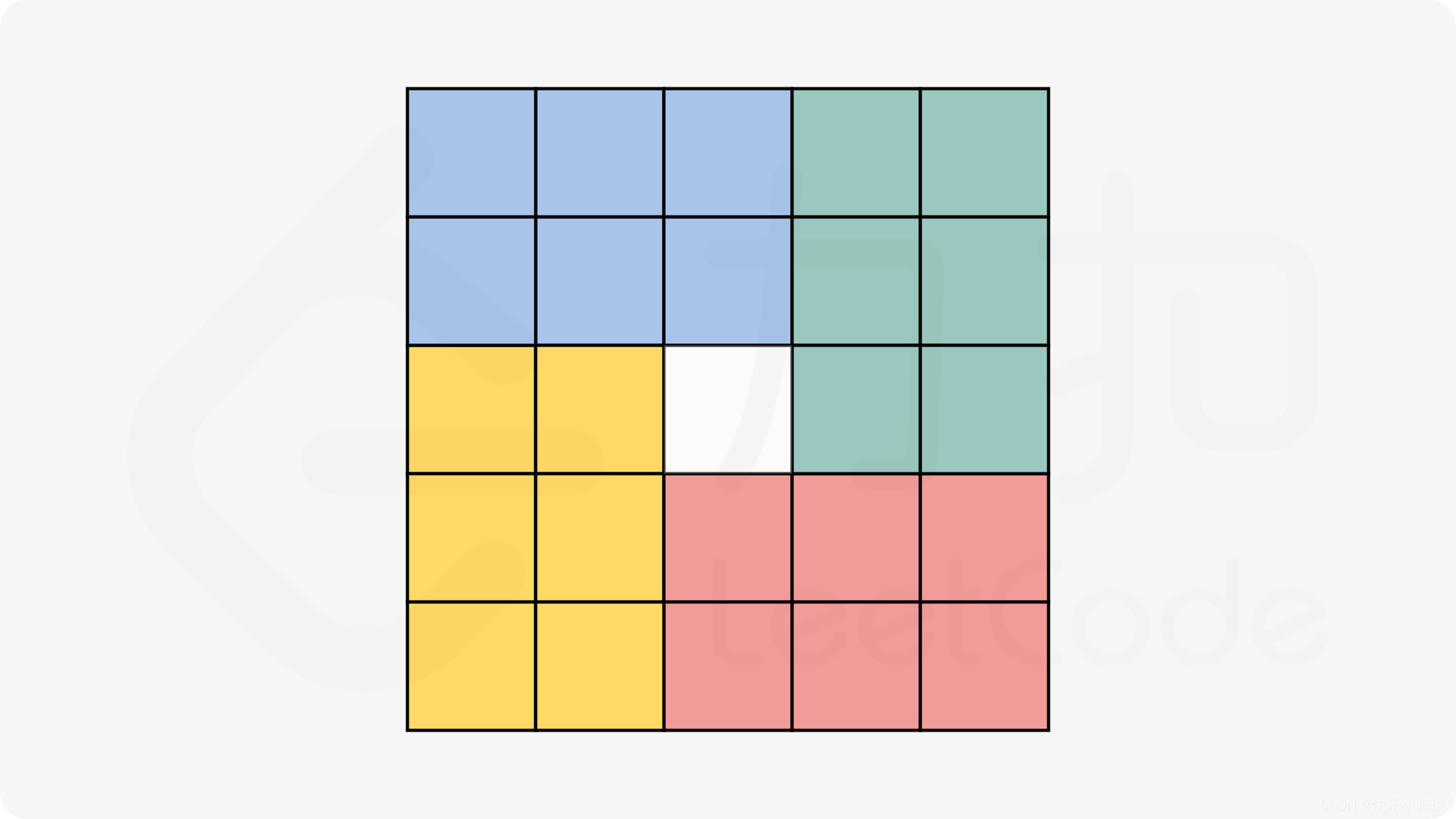
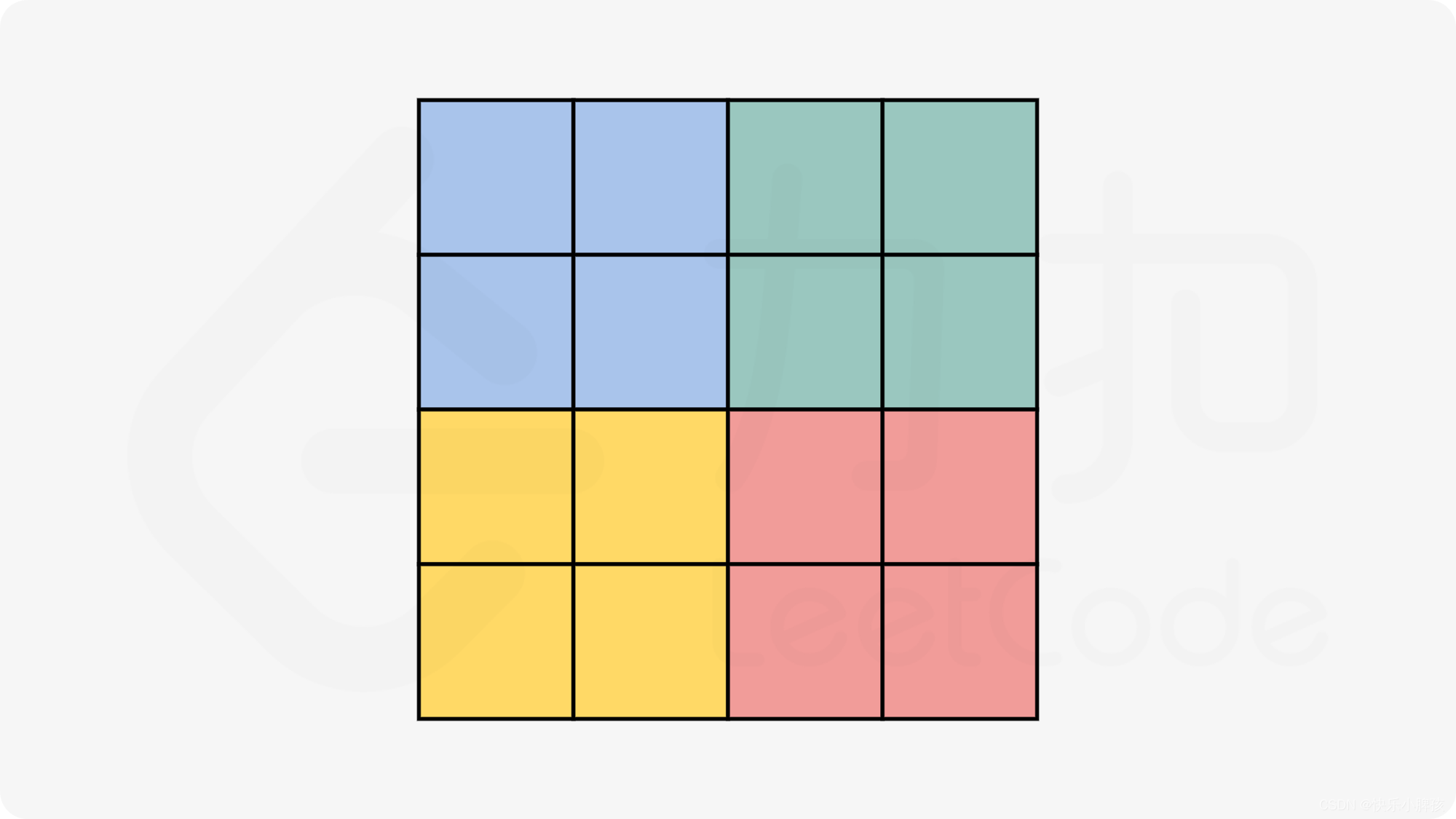
void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        int temp;
        for(int i = 0;i<n/2;i++){
            for(int j = 0;j<(n+1)/2;j++){
                temp = matrix[i][j];
                matrix[i][j] = matrix[n-j-1][i];//matrix[i][j]位置为matrix[n-j-1][i]旋转而来
                matrix[n-j-1][i] = matrix[n-i-1][n-j-1];//matrix[n-j-1][i]位置由matrix[n-i-1][n-j-1]旋转而来
                matrix[n-i-1][n-j-1] = matrix[j][n-i-1];//matrix[n-i-1][n-j-1]位置由matrix[j][n-i-1]旋转而来
                matrix[j][n-i-1] = temp;//matrix[j][n-i-1]位置由matrix[i][j]旋转而来,即为temp
            }
        }
    }

方法三：用翻转代替旋转
通过方法一可知我们matrix[i][j]旋转后的位置为matrix[j][n-i-1]，但是如果直接让matrix[j][n-i-1] = matrix[i][j]，会丢失matrix[j][n-i-1]的值，导致后面旋转matrix[j][n-i-1]时候发生错误，因此我们不考虑让一个一个元素变到对应的位置，我们考虑让所有元素一起变到对应的位置。
从以上思路可得，我们想要把matrix[i][j]变到matrix[j][n-i-1]，需要分两步：
1.把matrix[i][j]变到matrix[j][i]
2.把matrix[j][i]变到matrix[j][n-i-1]
或者是：
1.把matrix[i][j]变到matrix[n-i-1][j]
2.把matrix[n-i-1][j]变到matrix[j][n-i-1]
我们考虑第一种方案，我们如何实现1呢，可知我们对把矩阵的所有元素对主对角线对称，可以实现把matrix[j][i] = matrix[i][j]
然后我们把每一行元素翻转，即可得到matrix[j][n-i-1] = matrix[i][j],最终可实现matrix[i][j]变到matrix[j][n-i-1]，而不会覆盖元素，因为我们把原问题分解成了2个子问题。
时间复杂度：o(n2)
空间复杂度：o(1)

void rotate(vector<vector<int>>& matrix) {
       int n = matrix.size();
       int temp;
       //第一步，将原矩阵关于主对角线翻转
       for(int i=0;i<n;i++){
           for(int j=0;j<i;j++){
               swap(matrix[i][j],matrix[j][i]);
           }
       }
        //第二步，将原矩阵每一列翻转
        for(int i=0;i<n;i++){
            for(int j=0;j<n/2;j++){
                swap(matrix[i][j],matrix[i][n-j-1]);
            }
        }
    }