老卫带你学---leetcode刷题(29. 两数相除)

29. 两数相除

问题

给你两个整数，被除数 dividend 和除数 divisor。将两数相除，要求 不使用 乘法、除法和取余运算。

整数除法应该向零截断，也就是截去（truncate）其小数部分。例如，8.345 将被截断为 8 ，-2.7335 将被截断至 -2 。

返回被除数 dividend 除以除数 divisor 得到的 商 。

注意：假设我们的环境只能存储 32 位 有符号整数，其数值范围是 [?231, 231 ? 1] 。本题中，如果商 严格大于 231 ? 1 ，则返回 231 ? 1 ；如果商 严格小于 -231 ，则返回 -231 。

示例 1:

输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = 3.33333… ，向零截断后得到 3 。
示例 2:

输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = -2.33333… ，向零截断后得到 -2 。

提示：

-231 <= dividend, divisor <= 231 - 1
divisor != 0

解决

让我们先回顾一下小学时，怎么通过列竖式的方法计算两个整数的除法，以 45/2 为例：

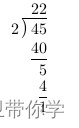
仔细观察不难发现，这种算法是把除法化归成移位和减法两种运算方法。对于 10 进制数，移位运算就是乘（左移）除（右移）10，而我们都知道计算机中的移位运算是乘（左移）除（右移）2，因为计算机是通过二进制的方法存储数的。这样，类比十进制，二进制的除法（仍以 45/2 为例）可以写作（注意，这里我们并没有用到乘除法）

解决

用二进制除法来做，逐步求出1的位数，然后得到十进制

def divide(self, dividend: int, divisor: int) -> int:
    sign = (dividend > 0) ^ (divisor > 0)
    dividend = abs(dividend)
    divisor = abs(divisor)
    count = 0
    #把除数不断左移，直到它大于被除数
    while dividend >= divisor:
        count += 1
        divisor <<= 1
    result = 0
    while count > 0:
        count -= 1
        divisor >>= 1
        if divisor <= dividend:
            result += 1 << count #这里的移位运算是把二进制（第count+1位上的1）转换为十进制
            dividend -= divisor
    if sign: result = -result
    return result if -(1<<31) <= result <= (1<<31)-1 else (1<<31)-1