算法与数据结构之链表＜一＞（Java）

2024-01-08 11:32:08

1、链表的定义

链表通过指针将一组零散的内存块串联在一起。其中，我们把内存块称为”结点“。为了将所有的结点串起来，每个链表的结点除了存储数据之外，还需要记录链上的下一个结点的地址。

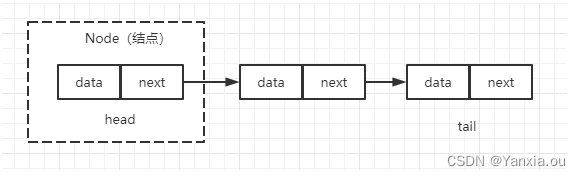
2、链表的特点

（1）不需要连续的内存空间
（2）有指针引用
（3）三种常见的链表结构：单链表、双链表、循环链表、（跳表：不常见但是功能强大，用到的地方也很多，比如redis，可以了解一下）
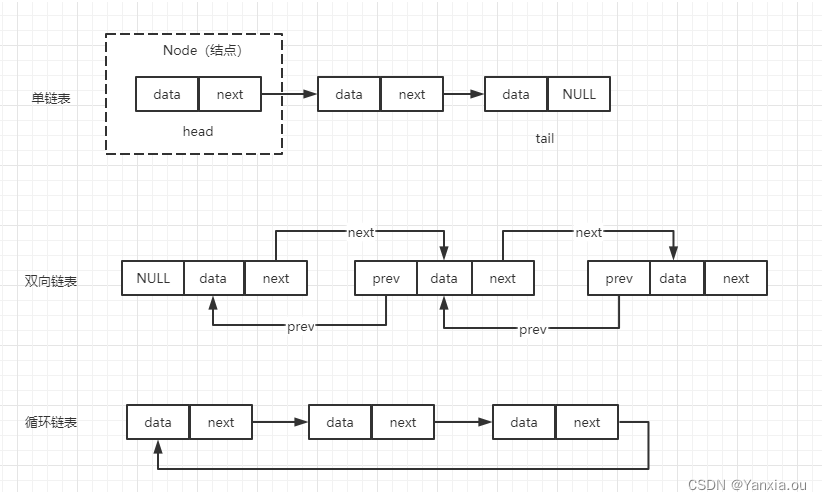
单链表： 第一个结点和最后一个结点分别为头结点和尾结点。头结点用来记录链表的基地址，有了它，我们就可以遍历得到整条链表。而尾结点的特殊地方是：指针不是指向下一个结点，而是指向一个空地址NULL，表示这是链表上的最后一个结点。
双向链表： 单向链表只有一个方向，结点只有一个后继指针next指向后面的结点。双向链表，顾名思义，它支持两个方向，每个结点不止有一个后继指针next指向后面的结点，还有一个前驱指针prev指向前面的结点。双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。缺点：如果存储同样多的数据，双向链表要比单链表占用更多的内存空间。优点：可以支持双向遍历，操作灵活（特别是对于范围查询有明显的优势、大于、小于）。实际应用：如 B+Tree（MySQL索引的叶子节点，采用的就是双向链表结构）
循环链表： 循环链表就是一种特殊的单链表。实际上，循环链表与单链表的唯一区别就是尾节点。单链表的尾节点指针指向空地址，表示这就是最后的结点了，而循环链表的尾结点指针是指向链表的头结点，形成一个环一样首尾相连的链表，所以"循环"链表。（约瑟夫问题）

3、为何要使用链表

稀疏数组：一般是针对多维数组
?1?2??4 -1
-1?3??5 -1
-1 1 -1 -1
a[3][4]：这是一个二维数组，-1表示存储的数据为空，已开空间大小3*4=12，稀疏数组就是真正存的数据远远小于我们开的空间，为了节省空间，往往会用链表代替。

4、数组与链表的区别

重要区别：
（1）数组简单易用，在实现上使用的是连续的内存空间，可以借助CPU的缓存机制（缓存行、缓存局部性），预读数组中的数据，所以访问效率更高。
（2）链表在内存中并不是连续存储，所以对CPU缓存不友好，没办法有效预读。
（3）数组的缺点就是大小固定，一经声明就要占用整块连续内存空间。如果声明的数组过大，系统可能没有足够的连续内存空间分配给它，导致"内存不足（Out Of Memory）"。如果声明的数组过小，则可能出现不够用的情况。
（4）动态扩容：数组需再申请一个更大的内存空间，把原数组拷贝过去，非常费时。链表本身没有大小限制，天然支持动态扩容。（但是链表不断的扩容会把内存撑爆，使用时需要注意）

5、链表的增删查

单向链表结构：头结点，指针（指向下一节点），value（存储的值），size已存储值的数量 
    public class MyLinkedList {
        private int size;
        ListNode head;

        class ListNode { //定义链表结构
            int value;
            ListNode next;

            ListNode(int value) { //构造函数，用于构造一个结点
                this.value = value;
                this.next = null;
                head = null;
            }
        }
    }

5.1、在头部插入链表

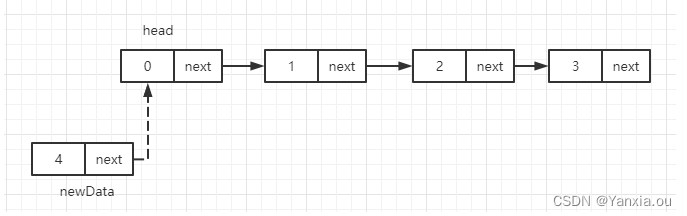
    private void insertHead(int data) {//时间复杂度O(1)
        ListNode newData = new ListNode(data);//构造一个结点
        newData.next = head; //栈内存的引用
        head = newData;
        size++;
    }

5.2、在中间插入链表

 private void insertNth(int data, int position) {//插入链表的中间，假设定义在第N个插入，O(n)
        if (position == 0){//这里表示插入在头部
            insertHead(data);
        } else {
            ListNode newData = new ListNode(data);
            ListNode curr = head;
            for (int i=0; i< position; i++){
                curr = curr.next;//一直往后遍历，找到要插入的位置,c/c++的 p=p->next;
            }
            //确保链表不会断裂丢失数据
            newData.next = curr.next;//先将新加的结点指向后面，保证不断链
            curr.next = newData;//把当前的点指向新加的点
        }
        size++;
    }

5.3、删除头节点

    private void deleteHead(int data) {//O(1)
        head = head.next;
        size--;
    }

5.4、删除中间节点

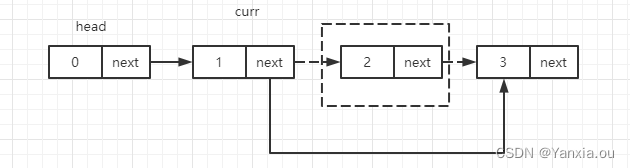
   private void deleteNth(int data, int position) {//O(1)
        if (position == 0){
            deleteHead(data);
        } else {
            ListNode curr = head;
            for (int i=0; i< position; i++){
                curr = curr.next;
            }
            curr.next = curr.next.next;//curr.next 表示的是删除的点
        }
        size--;
    }

5.5、查询某个值

    public void find(int data){//O(n)
        ListNode cur = head;
        while(cur != null){//判断不是尾结点
            if(cur.value == data) break;//找到后退出循环
            cur = cur.next;//遍历下一个结点
        }
    }

6、链表的应用

6.1 如何设计一个LRU缓存算法？

LRU（Least Recently Used：最近最少使用，它主要思想是当缓存空间占满时，移除最近最少使用的缓存对象） 
    /**
     * 1、先判断链表中是否已存在该data，如果已存在则抛弃旧的值，然后在head插入新的值
     * 2、如果不存在改data，则直接在head插入该data，保证head为最新访问的值
     * 这里实现的是简单的lru，深层次的lru可使用哈希表+双向链表实现（可参考力扣的题目）
     * @param data
     */
    private void lru (int data) {
        ListNode newData = new ListNode(data);
        ListNode curr = head;
        while (curr.next != null) {
            if (curr.value == data){
                //删除该结点
                curr.next = curr.next.next;
                break;
            }
            curr = curr.next;
        }
        //插入链表头部
        head = newData.next;
    }

6.2 约瑟夫问题

读者可以先思考此问题的实现，该问题的求解过程小编会在另一篇博文解答，敬请期待！！

详见博文：数据结构与算法之约瑟夫问题求解-CSDN博客

文章来源:https://blog.csdn.net/m0_58476313/article/details/135380318
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。