python之使用蒙特卡洛方法估计圆周率π
2023-12-13 18:36:41
import random
import matplotlib.pyplot as plt
def monte_carlo_pi(num_samples):
inside_circle = 0
inside_x, inside_y = [], []
outside_x, outside_y = [], []
for _ in range(num_samples):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
distance = x**2 + y**2
if distance <= 1:
inside_circle += 1
inside_x.append(x)
inside_y.append(y)
else:
outside_x.append(x)
outside_y.append(y)
pi_estimate = 4 * (inside_circle / num_samples)
return pi_estimate, inside_x, inside_y, outside_x, outside_y
# 设置随机生成点的数量
num_samples = 1000
# 运行蒙特卡洛方法
estimated_pi, inside_x, inside_y, outside_x, outside_y = monte_carlo_pi(num_samples)
# 绘制散点图和单位圆
fig, ax = plt.subplots()
ax.scatter(inside_x, inside_y, color='blue', label='Inside Circle')
ax.scatter(outside_x, outside_y, color='red', label='Outside Circle')
ax.set_aspect('equal', 'box')
circle = plt.Circle((0, 0), 1, edgecolor='black', facecolor='none', linewidth=2, label='Unit Circle')
ax.add_patch(circle)
ax.legend()
# 显示估计的π值
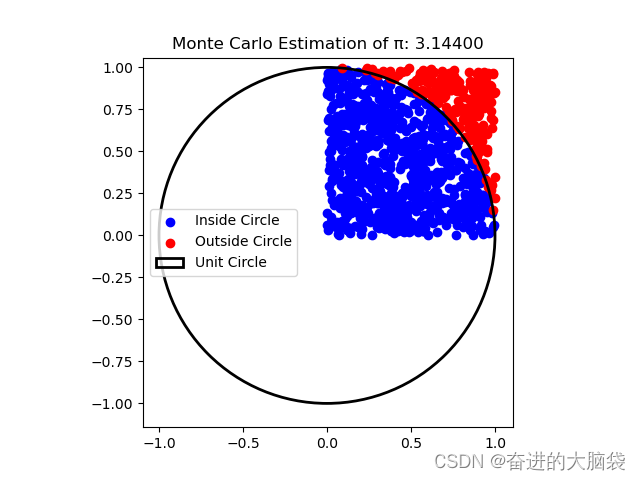
plt.title(f"Monte Carlo Estimation of π: {estimated_pi:.5f}")
plt.show()
估计图:
文章来源:https://blog.csdn.net/qq_42244167/article/details/134883752
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!