0/1背包问题
2023-12-16 21:52:32
实验要求
随机生成500个0/1背包问题(问题规模可以相对较小),分别使用贪心算法和动态规划进行求解,
要求:1)统计贪心算法求得最优值的概率,
2)计算比值
3)应用贪心算法求解时,统计最坏的情况下误差有多大,
4)实验结果跟实验设置的参数(如:背包容量、物品的体积)关系很大,简要分析参数对结果的影响。
设计分析
对0-1背包问题,可以设计多种贪心策略,如:
重量最轻的物品优先的贪心策略。
价值最大的物品优先的贪心策略。
单位价值最大的物品优先的贪心策略。
随机选择物品的贪心策略。
无法数学证明某一种策略的最优性,因此使用贪心法求解0-1背包问题时,必须尽可能多地枚举各种贪心策略,并从各种贪心策略的运行结果中,找出问题的近似最优解。
算法描述
根据每个物品的单位价值(即价值/体积),将物品从高到低排序。
依次考虑每个物品,若该物品的体积小于等于背包剩余容量,则将该物品放入背包中,并更新剩余容量。
若该物品的体积大于背包剩余容量,则将该物品不放入背包,考虑下一个物品。
重复步骤2-3,直到所有物品都被考虑完毕,或者背包容量已经全部用完为止。
该贪心算法的核心思想是:每次选择单位价值最大的物品放入背包中,这样可以保证在背包容量充足的情况下,每次放入物品都能使背包价值最大化。
源码:
import random
# 生成一个背包问题
def generate_knapsack_problem(n, max_volume, max_weight):
# 物品数量
items = list(range(1, n+1))
# 物品体积和价值
volumes = [random.randint(1, max_volume) for _ in items]
values = [random.randint(1, max_weight) for _ in items]
# 背包容量
capacity = random.randint(max_volume, max_volume*2)
return items, volumes, values, capacity
# 贪心算法求解0/1背包问题
def greedy_knapsack(items, volumes, values, capacity):
n = len(items)
ratios = [(i, values[i-1]/volumes[i-1]) for i in items]
ratios.sort(key=lambda x: x[1], reverse=True)
selected_items = []
total_value = 0
for i, ratio in ratios:
if volumes[i-1] <= capacity:
selected_items.append(i)
total_value += values[i-1]
capacity -= volumes[i-1]
return selected_items, total_value
# 动态规划算法求解0/1背包问题
def dp_knapsack(items, volumes, values, capacity):
n = len(items)
dp = [[0] * (capacity+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, capacity+1):
if volumes[i-1] > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-volumes[i-1]] + values[i-1])
selected_items = []
j = capacity
for i in range(n, 0, -1):
if dp[i][j] > dp[i-1][j]:
selected_items.append(i)
j -= volumes[i-1]
selected_items.reverse()
return selected_items, dp[n][capacity]
# 随机生成500个背包问题并求解
n_problems = 500
max_volume = 100
max_weight = 100
greedy_success = 0
total_ratio = 0
worst_ratio = 0
worst_error = 0
for i in range(n_problems):
items, volumes, values, capacity = generate_knapsack_problem(10, max_volume, max_weight)
greedy_items, greedy_value = greedy_knapsack(items, volumes, values, capacity)
dp_items, dp_value = dp_knapsack(items, volumes, values, capacity)
# 统计贪心算法求解最优值的概率
if greedy_value == dp_value:
greedy_success += 1
# 计算贪心算法和动态规划算法求解结果的比值
ratio = greedy_value / dp_value
total_ratio += ratio
# 计算贪心算法求解最差情况下的误差
if len(dp_items) > len(greedy_items):
worst_ratio += 1
worst_error += dp_value - greedy_value
# 输出统计结果
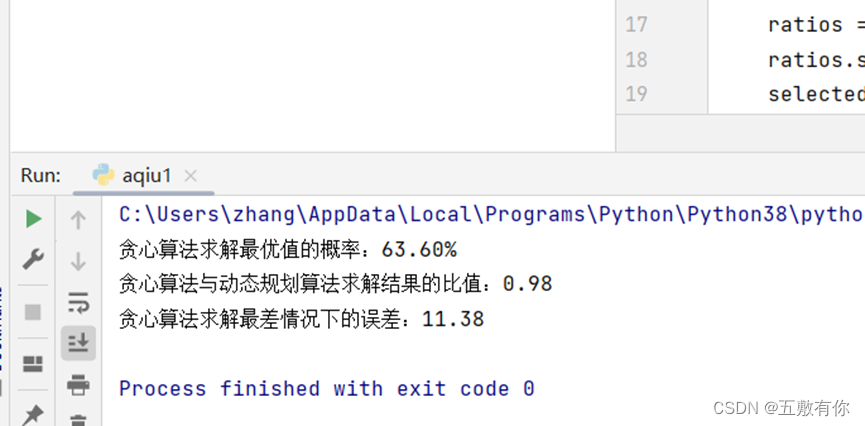
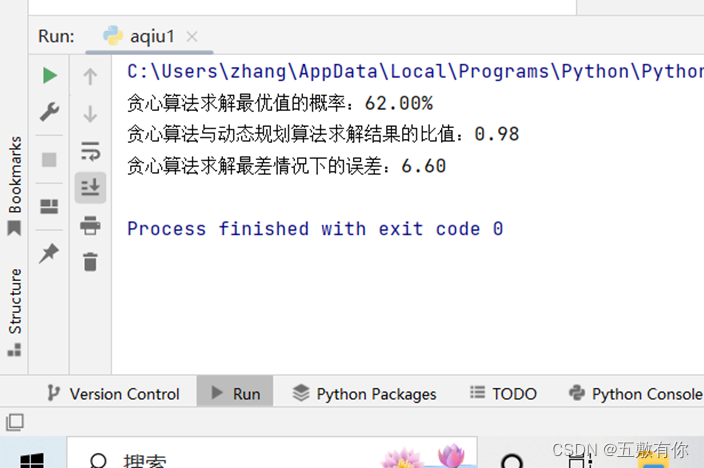
print(f"贪心算法求解最优值的概率:{greedy_success/n_problems:.2%}")
print(f"贪心算法与动态规划算法求解结果的比值:{total_ratio/n_problems:.2f}")
print(f"贪心算法求解最差情况下的误差:{worst_error/worst_ratio:.2f}")
实验结果
文章来源:https://blog.csdn.net/m0_62645012/article/details/135037367
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!