【百度PARL】强化学习笔记
文章目录
视频:世界冠军带你从零实践强化学习
代码:github仓库
因项目需要,这系列课程只学到了DQN。本人首先先学习了李宏毅的policy-based的课程,然后再学习这里百度飞桨科科老师的强化学习课程,主要学习了value-based的内容。科科老师这里对代码逻辑的讲解更加清晰,非常的好。
强化学习基本知识

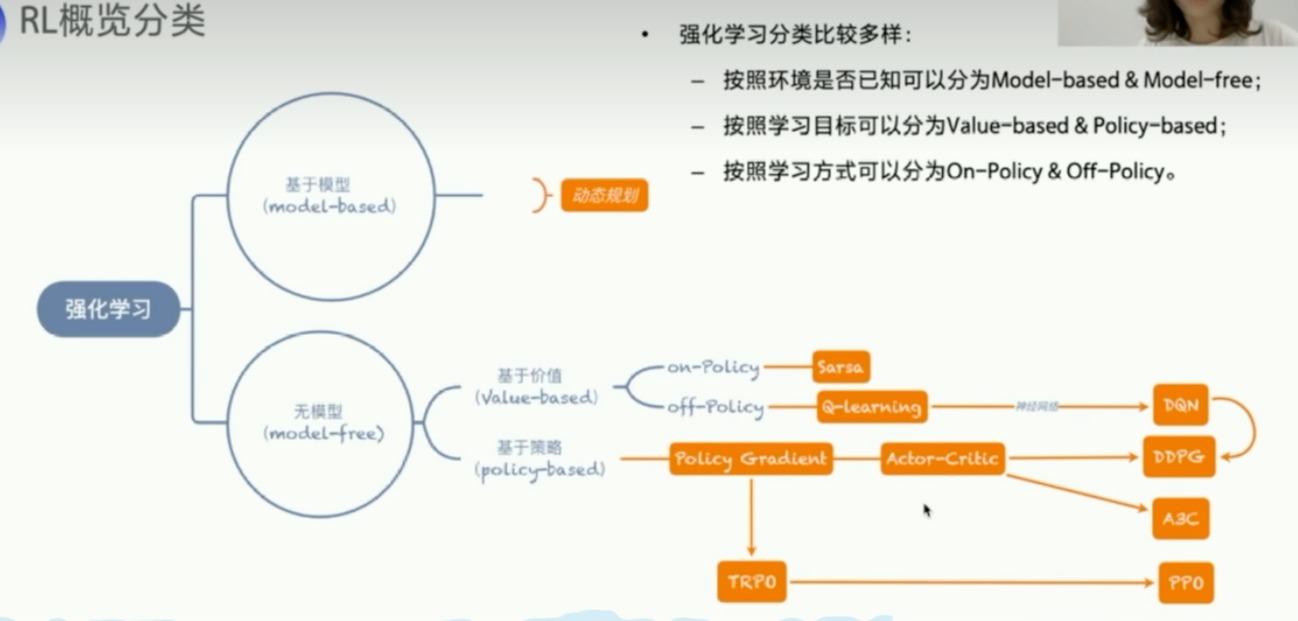
- 算法库

一些框架
- PARL
- 对于一个新的example,只需要修改一下agent/model就可以了
- 算法在parl文件夹中也将所有算法定义好了

- 第一部分总结
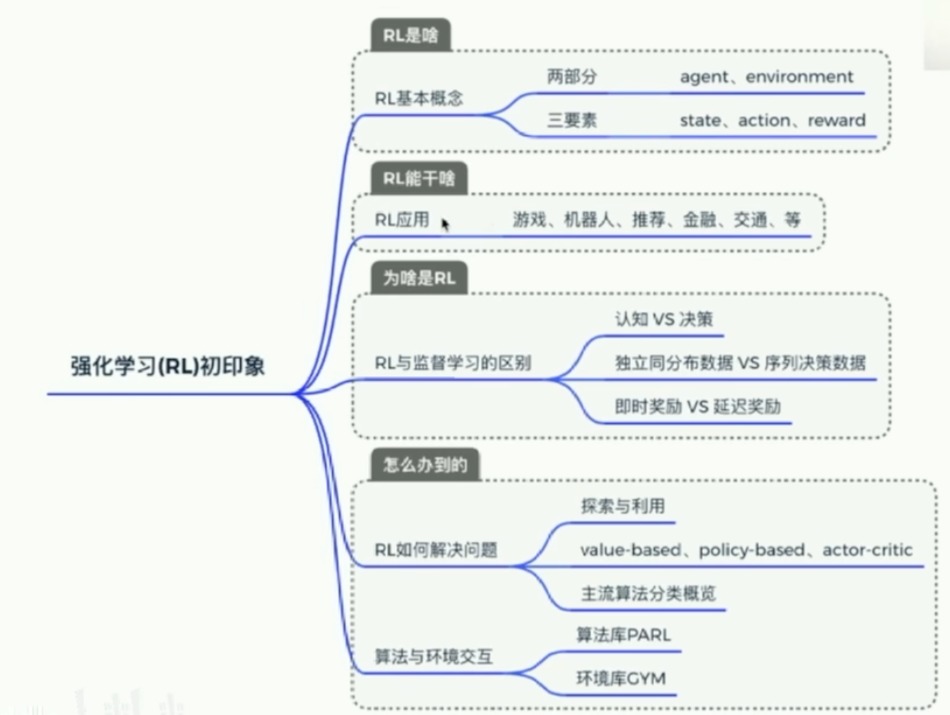
Value-based的方法
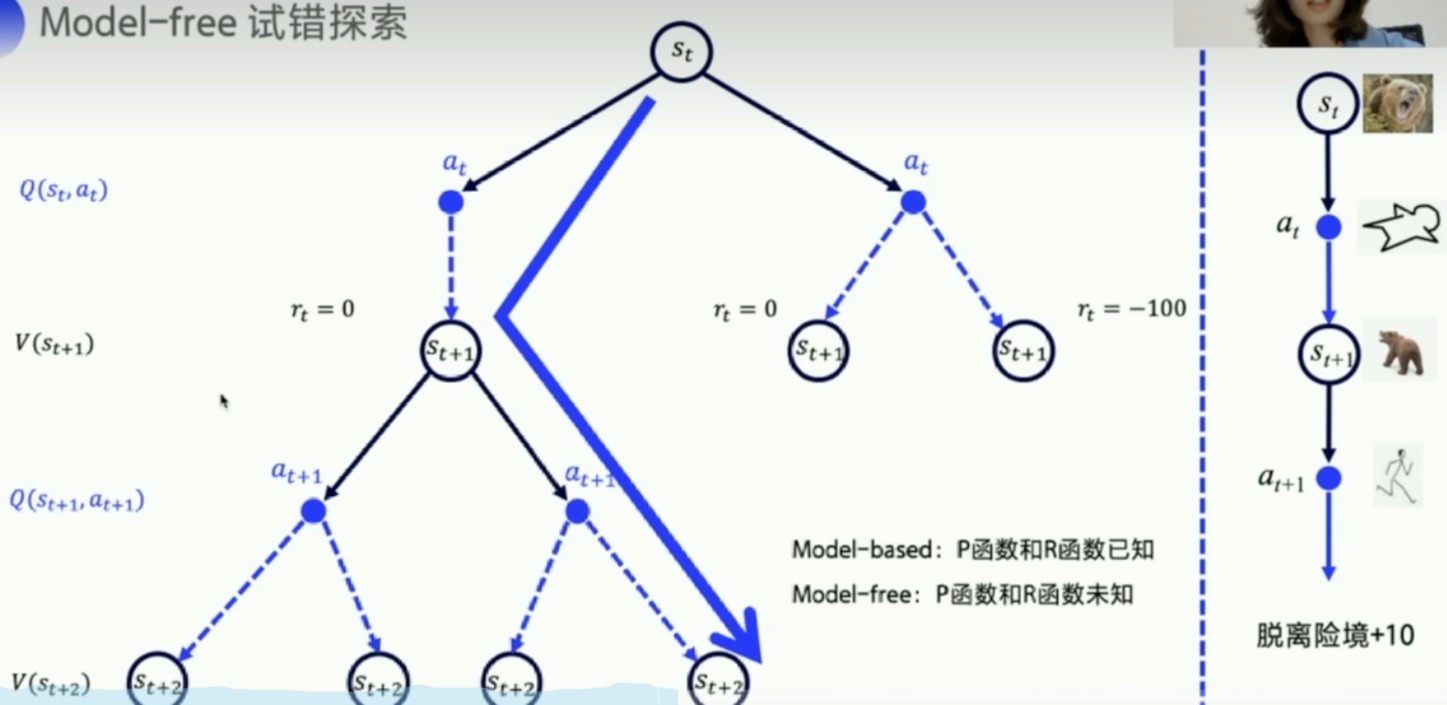
下图的过程是符合马尔科夫决策过程的,俗称MDP
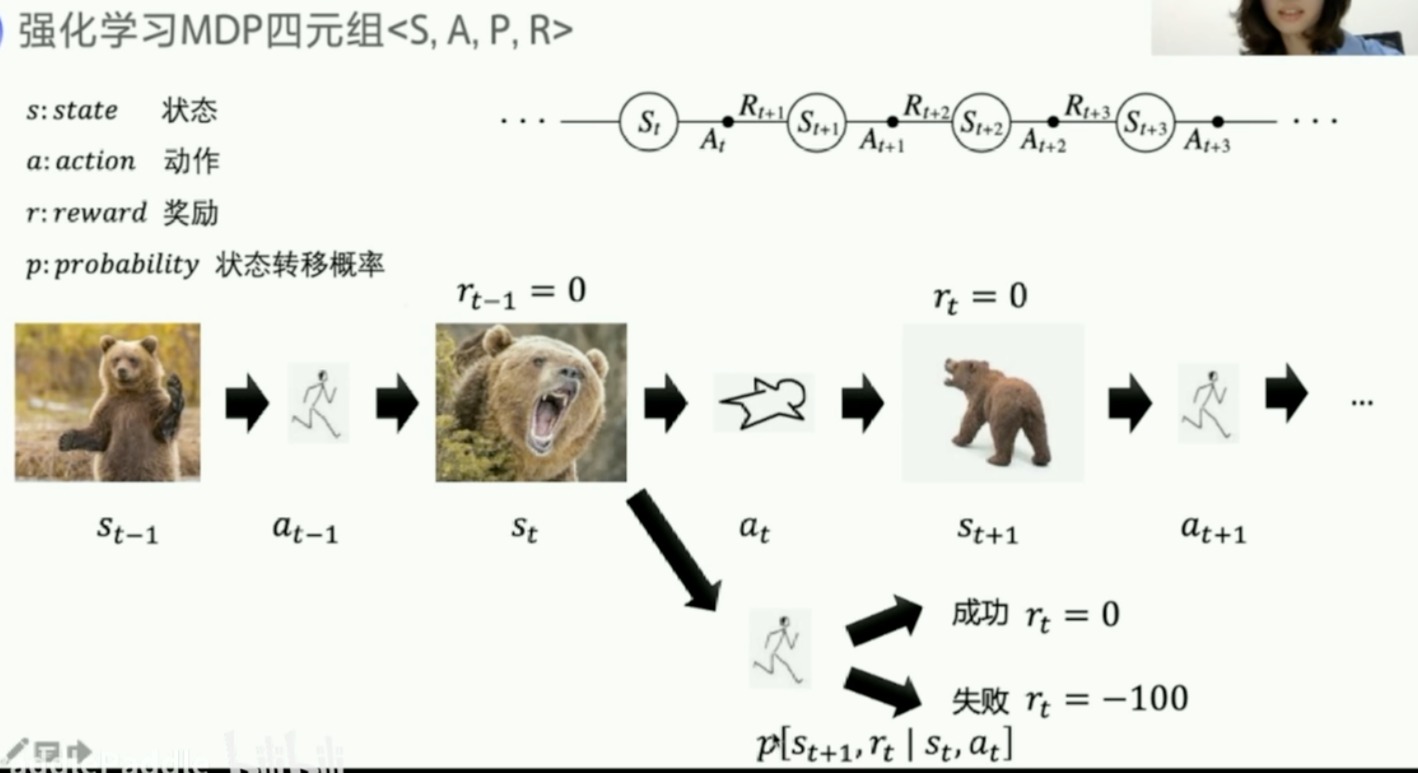
- 如果状态转移概率和reward都是已知的,那么就称这个环境是已知的
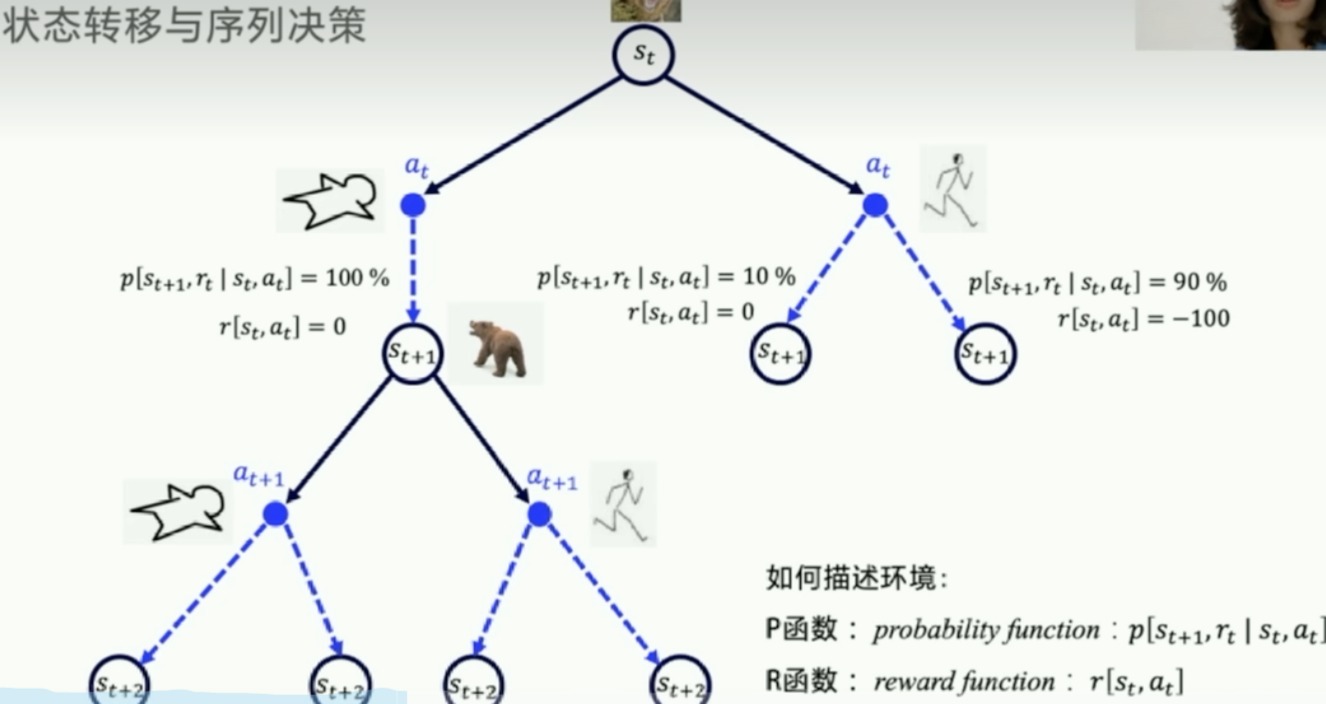
- model-based
- P函数和R函数已知
- 可以直接用动态规划求解
- model-free
- P函数和R函数未知
- 试错探索,现实世界的环境往往未知
- 我们主要学习这个
- 用Q函数和V函数来表示
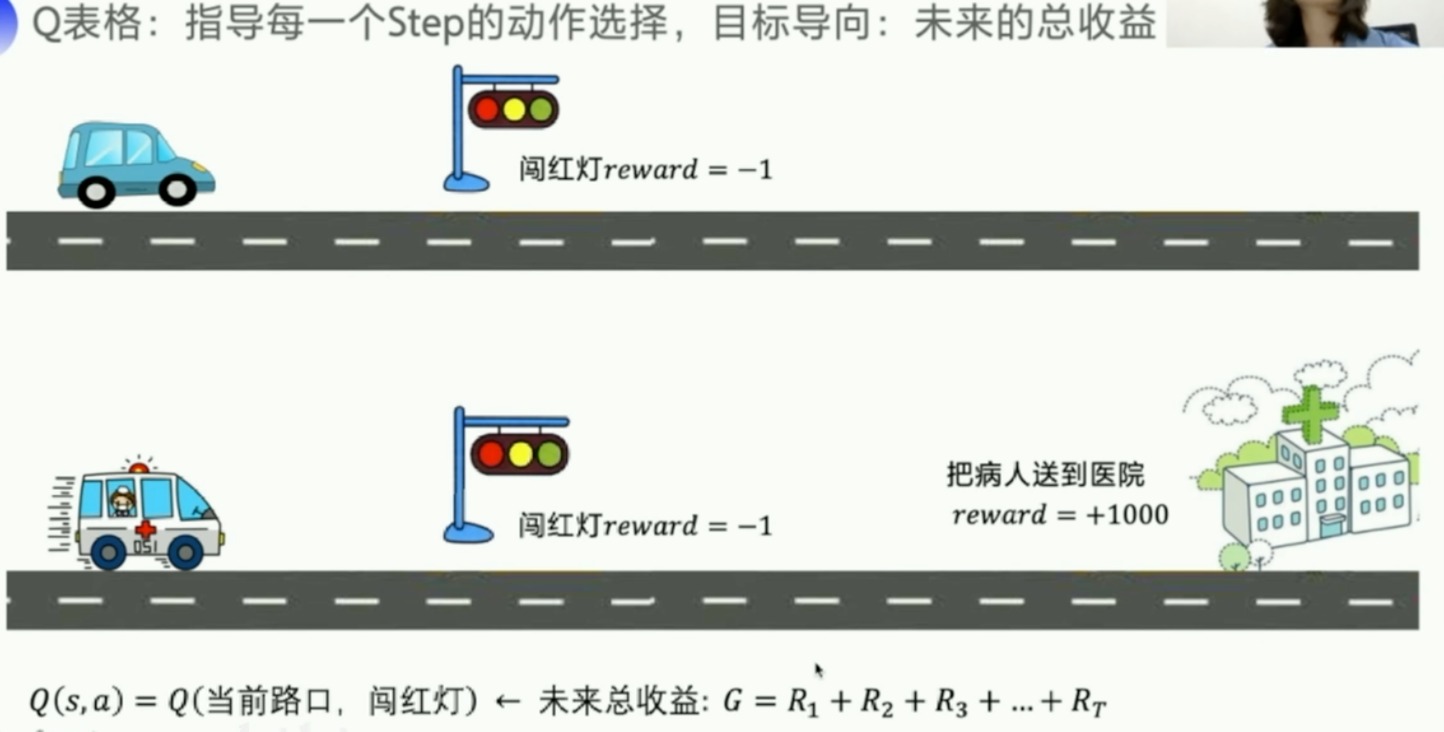
Q表格
反应在某个s下,哪个动作价值高

Q表格:指导每一个Step的动作选择,目标导向:未来的总收益
我们的收益要看的更远一些
但是有时候看的太远也不好,所以引入衰减因子 γ \gamma γ

举个例子
- 折扣因子

- 我们就是要求解Q表格
- 刚开始全部初始化为0,当足够多的与环境交互之后,Q表格就会更新足够完善
强化的概念
-
时序差分
- 主要特点是在估计当前策略的价值函数时,它不需要等到一个完整的序列(如一局游戏)结束后才更新价值估计,而是在每一步之后立即进行更新
- 李宏毅讲过
-
在不断的重复试验之后,原本是要看到熊发怒才会瑟瑟发抖,不断试验之后,看到有熊爪就会瑟瑟发抖
- 意味着agent学会了预测熊发怒这一状态的价值,并将这种预期的负面价值向前传播到先前的状态(熊爪)。这种向前传播的过程是通过Temporal Difference Error来完成的,这个错误是实际奖励和智能体预测的未来奖励之间的差异。智能体使用这个TD错误来更新其关于当前状态和动作的价值估计,使得未来的决策更加准确。
-
下一个状态的价值,是可以不断强化影响上一个状态的价值
- 下一个状态的价值只与当前状态有关,历史的状态已经融合到当前状态

- 状态价值迭代
- demo
- https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_td.html
TD更新
拿下一步的Q值去更新这一步的Q值
- 刚开始 Q ( S t , A t ) Q(S_t,A_t) Q(St?,At?)初始化为0,其要去逼近Target、也就是未来收益之和 G t G_t Gt?。
- 在做一个简单的数学变换我们可以发现
- G t G_t Gt? = R t + 1 + γ G t + 1 R_{t+1}+{\gamma}G_{t+1} Rt+1?+γGt+1?
- 因为 Q ( S t , A t ) Q(S_t,A_t) Q(St?,At?)要逼近 G t G_t Gt?
- 所以差不多 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1?,At+1?)要逼近 G t + 1 G_{t+1} Gt+1?
- α:学习率,决定了新信息覆盖旧信息的速度
- 当前的Q值会向目标Q值逼近,而目标Q值是基于智能体获得的实际奖励和下一个状态-动作对的预期Q值计算得来的。
- 右侧的图表示了状态和动作之间的转移,以及如何更新Q值。每次智能体在状态 ( $S_t $) 下采取动作 ( A t A_t At? ),都会转移到新的状态 ( $S_{t+1} KaTeX parse error: Can't use function '\)' in math mode at position 1: \?)? 并采取新的动作 \( A_{t+1} $),同时接收奖励 ( $R_{t+1} $),然后基于这些信息来更新Q值。

所谓的软更新其实像一种误差,表示预期(即时奖励加上对下一状态的Q值的估计)与当前估计之间的差异
预期反映了采取动作 A t A_t At? 并进入状态 S t + 1 S_{t+1} St+1? 后的长期期望回报
在时序差分(TD)学习中,如果 ( R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) Rt+1?+γQ(St+1?,At+1?) ) (也就是我们说的目标或者预期)比当前的 ( Q ( S t , A t ) Q(S_t, A_t) Q(St?,At?) ) 低,这并不能直接告诉我们是当前的动作 ($ A_t $) 有问题还是下一步的动作 ( A t + 1 A_{t+1} At+1?) 有问题。这里涉及的是两个连续的决策(当前和未来)以及它们对长期回报的影响。
理解这个情况需要分析几个方面:
即时奖励 ( R t + 1 R_{t+1} Rt+1? ): 这是智能体在状态 ($ S_t$ ) 执行动作 ($ A_t$ ) 之后立即获得的奖励。如果这个奖励很低,它可能表明当前的动作并不理想。
未来预期回报 ($ \gamma Q(S_{t+1}, A_{t+1}) $): 这代表智能体预期在下一个状态 ( S t + 1 S_{t+1} St+1? ) 执行动作 ( A t + 1 A_{t+1} At+1? ) 之后能够获得的折扣后的回报。如果这个值低,它可能意味着从当前状态 ( $S_t $) 到达的下一个状态 ( $S_{t+1} KaTeX parse error: Can't use function '\)' in math mode at position 1: \?)? 不是一个有利的状态,或者在那… A_{t+1} $) 不是最佳选择。
TD误差: 如果 ( R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) Rt+1?+γQ(St+1?,At+1?) ) 比 ( Q ( S t , A t ) Q(S_t, A_t) Q(St?,At?) ) 小,TD误差是负的,这表明智能体对当前状态-动作对的价值估计过高。智能体需要通过学习降低这一估计,以更准确地反映实际的长期回报。
学习和策略改进: 这个信息(TD误差)被用来指导智能体如何调整其策略。如果TD误差反复为负,智能体会逐渐学习减少选择导致这种情况的动作的频率。相反,如果TD误差为正,智能体会增加选择那个动作的倾向。
在实际应用中,我们需要考虑整个学习过程,并且通常要运行多个episode来确定是否一种特定的动作序列通常导致负面的结果。只有在长时间和多次迭代的基础上,我们才能确定问题是否出在当前动作、下一动作,或者是整体策略的问题。
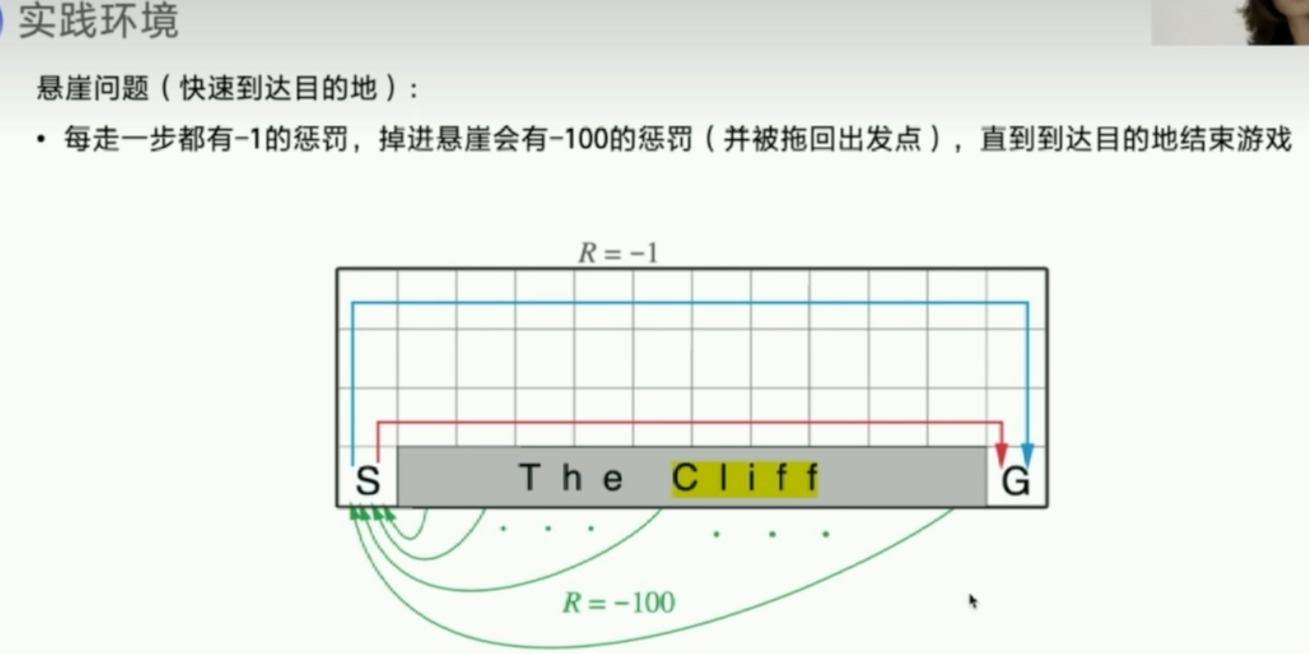
Sarsa算法
- 伪代码

不停的训练,Q就会收敛到某个状态
重点:注意Sarsa这里是根据next_obs先拿到next_action。这跟Q-learning很不一样
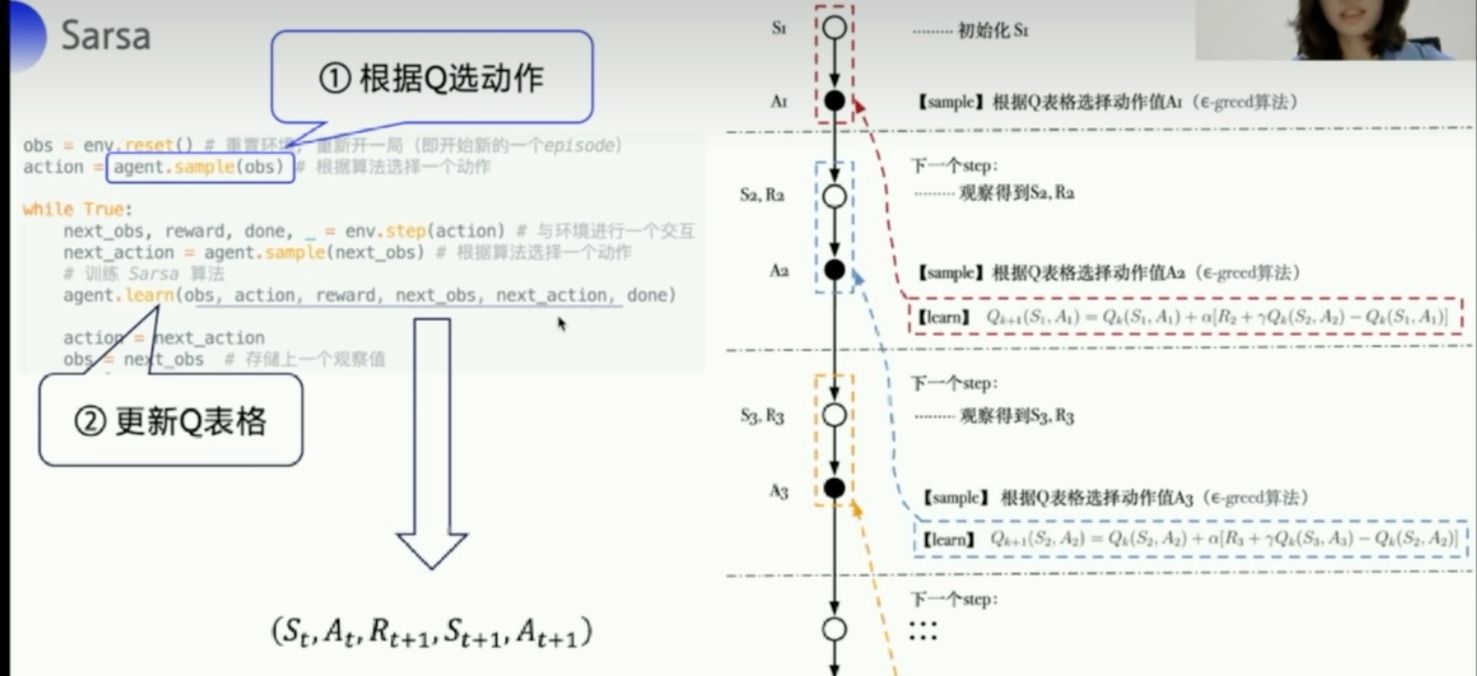
Sample
- predict函数
- 贪心算法,先提取出Q table中某个obs的一行,找出这行Q最大的格子。如果有多个格子,那就随机选取一个,并返回其对应的action
- 但是这样子agent不会探索,所以我们使用sample函数
- 除了我们能拿到最优的动作外,还有一定的概率能探索到别的action

所以整个训练的代码是这样子的
最重要的就是左边流程图红框框的这个

agent主要就是两个功能,一个是sample、一个是learn。learn后面会讲,对Q表格进行更新
Sarsa Agent类
- 初始化
- obs的维度和act维度

- learn 更新Q表格的方法
- 就是完全按照那个公式来的,先求出目标Q,然后对当前Q进行修正

- 结合上环境,具体例子,调包的代码

On_policy vs off_policy
强化学习中on-policy 与off-policy有什么区别?
- 目标策略
- 比如说Q表格训练完之后,我们对于一个s,去找到对应Q值最大的a,的这个决策过程,叫做目标策略
- 行为策略
- 进行数据的收集的策略是行为策略

q learning 并没有实际上要传进来的那个值
传进来下一个next action
q learning更大胆,默认自己选的就是最优的
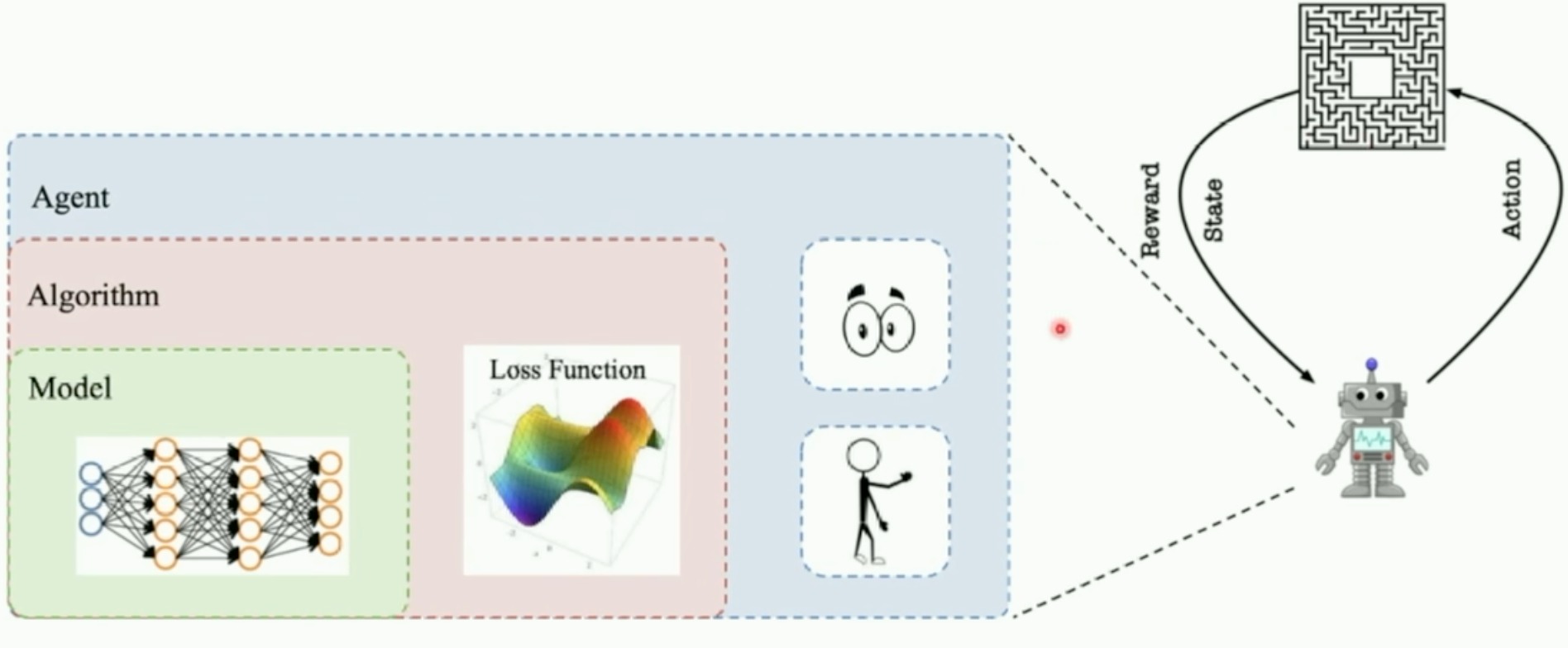
函数逼近与神经网络
- 因为很多情况下,state太多了,Q表格存不下,这时候可以用值函数来近似

复习一下Q-learning
其实这里Q的更新就是用下一步的Q来更新上一步的Q,去逼近这个未来的Reward。
其中对于action的选择,是有sample策略的

- DQN的改进就是把Q表格给换成了神经网络
- 输入一个s,通过神经网络,输入所有的action的Q值

DQN算法
DQN创新点
用神经网络来代替Q表格,会引发两个问题,DQN使用两个方法解决了以下两个问题
- 经验回放:样本相关性
- 序列决策的样本关联
- 样本利用率低
- 固定Q目标
- 非平稳性:算法非平稳
- 经验回放
- 不用连续数据训练


- 固定Q目标
- 解决了算法更新不平稳的问题

-
在DQN中,如果我们用同一个网络来选择最大化动作和评估这个动作的Q值,会有一个问题:网络的微小更新可能会极大地影响这个最大化动作的选择,导致训练变得非常不稳定
-
为了解决这个问题,DQN采用了固定Q目标技巧。具体来说,DQN使用两个网络:一个是行为网络,用于选择动作;另一个是目标网络,用于计算Q目标值。目标网络的权重是行为网络权重的较老版本,不会在每一步更新。在一定的时间步后,行为网络的权重会被复制到目标网络。这样可以使训练过程更加稳定,因为目标Q值变化不会那么剧烈。
-
DQN流程图
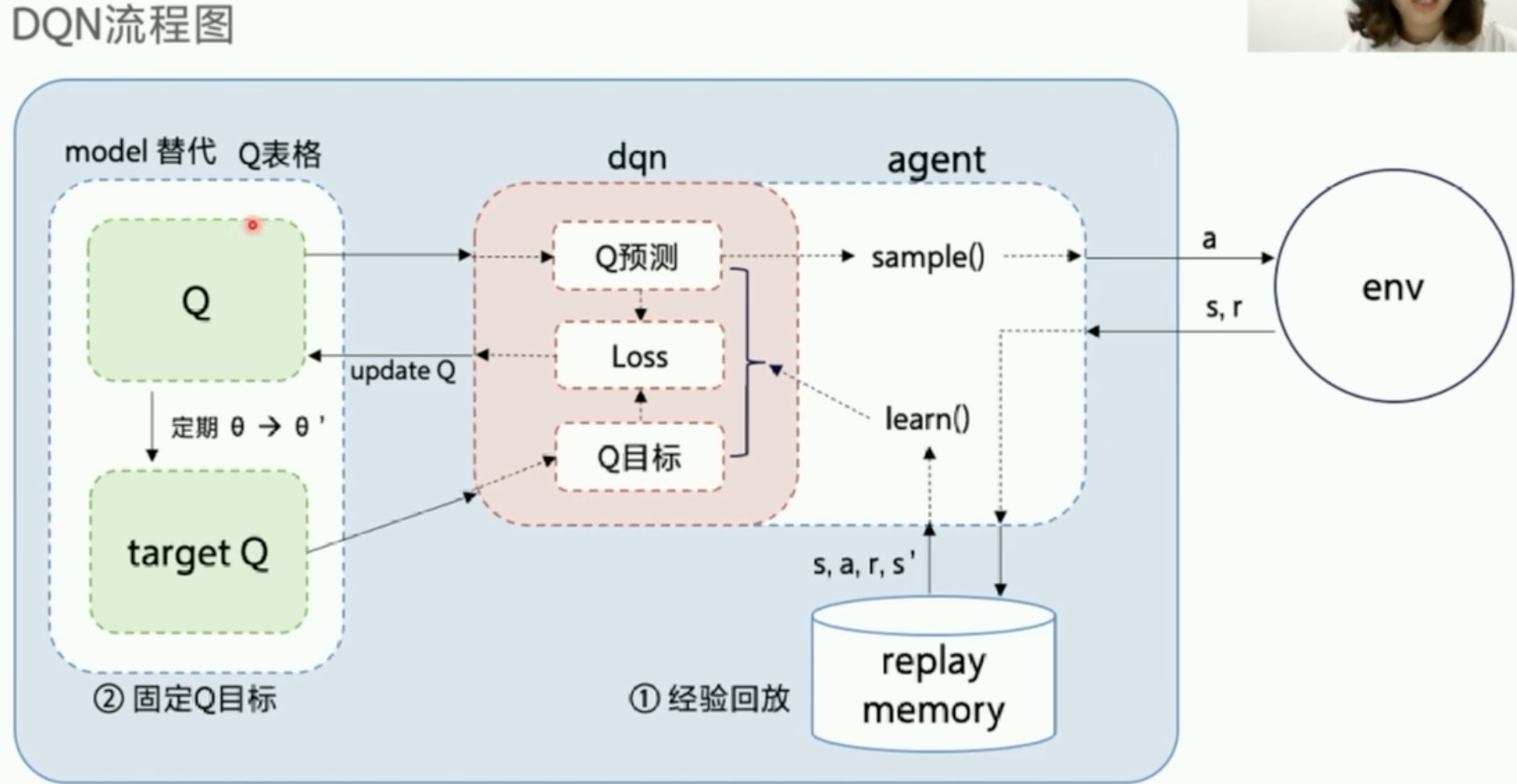
PARL的DQN框架
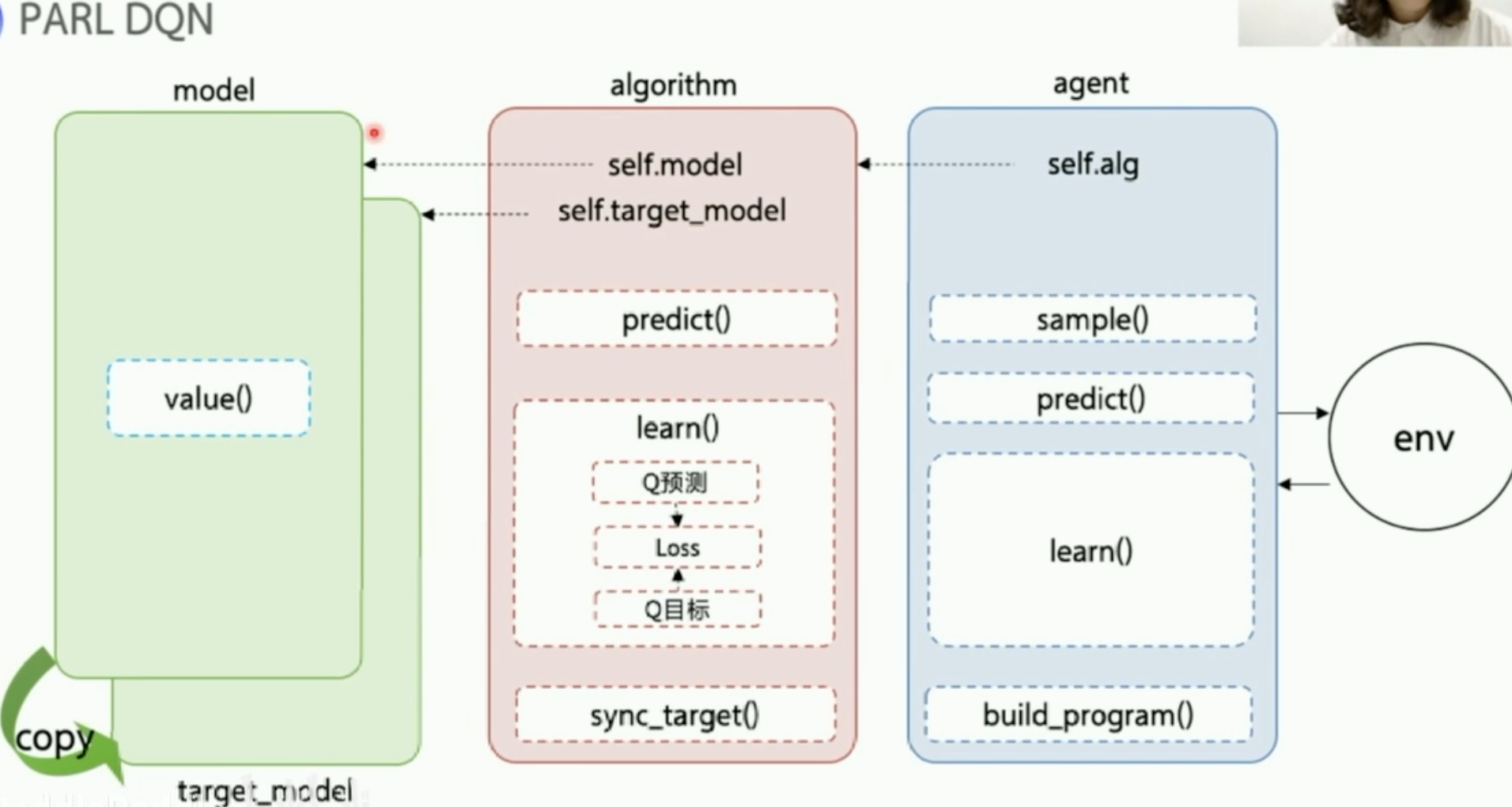
用嵌套的方式来组成这个agent
重点就是根据数据和模型结构来构建loss function这步做好了,就好用。
- 训练文件目录

一些补充:
Q:他如何计算目标Q,跟他实际下一步执行哪个action是没有关系的
A:对的,你理解得很准确。在DQN算法中,计算目标Q值的过程与智能体实际执行的下一步动作是独立的。
在DQN中,目标Q值的计算方式是基于贪婪策略的,即选取下一个状态(s’)中具有最大预期回报的动作(a’)的Q值。具体来说,它使用目标网络来预测下一个状态的所有可能动作的Q值,并从中选择最大的Q值来构建目标Q值。这个过程是基于对最优行为的假设,不考虑智能体实际采取的动作。
这样做的原因在于,DQN旨在学习一个最优策略,这个策略可以告诉智能体在任何给定状态下应该采取什么动作以最大化长期收益。通过总是考虑最优动作的Q值,DQN试图引导智能体学习如何在任何情况下都做出最佳决策。
然而,这并不意味着智能体在实际的操作中总是选择最佳动作。在实际执行过程中,智能体通常会采用?-greedy策略(即大部分时间选择最优动作,但有小概率随机选择一个动作)来平衡探索和利用。这样,智能体可以在执行过程中探索新的动作,而不是始终固守已知的最优动作。但在学习更新过程中,计算目标Q值时仍然是基于最优动作的假设。
DQN代码实现
model.py
主要就是实现value()函数,输出Q价值。
定义来三层网络结构,act_dim就是最后输出动作有多少,这里维度就是多少
import parl
from parl import layers # 封装了 paddle.fluid.layers 的API
class Model(parl.Model):
def __init__(self, act_dim):
hid1_size = 128
hid2_size = 128
# 3层全连接网络
self.fc1 = layers.fc(size=hid1_size, act='relu')
self.fc2 = layers.fc(size=hid2_size, act='relu')
self.fc3 = layers.fc(size=act_dim, act=None)
def value(self, obs):
h1 = self.fc1(obs)
h2 = self.fc2(h1)
Q = self.fc3(h2)
return Q
algorithm.py
DQN的类继承PARL里的algorithm
定义一个model,直接把前面定义的model拿过来,然后再deepcopy一下,作为目标网络
再定义一些超参数
import copy
import paddle.fluid as fluid
import parl
from parl import layers
class DQN(parl.Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" DQN algorithm
Args:
model (parl.Model): 定义Q函数的前向网络结构
act_dim (int): action空间的维度,即有几个action
gamma (float): reward的衰减因子
lr (float): learning_rate,学习率.
"""
self.model = model
self.target_model = copy.deepcopy(model)
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
assert isinstance(lr, float)
self.act_dim = act_dim
self.gamma = gamma
self.lr = lr
- sync_target()
- 实现定期参数同步,将self.model的参数同步到self.target_model
- 调用PARL中已经实现好的api即可
def sync_target(self):
""" 把 self.model 的模型参数值同步到 self.target_model
"""
self.model.sync_weights_to(self.target_model)
- predict()
- 使用model.value方法,来获取一批action在observation中对应的Q值
- 输出个数与输入的action个数一样
def predict(self, obs):
""" 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...]
"""
return self.model.value(obs)
-
learn()
-
最核心的方法
-
分为三部分
- 计算目标Q
- 计算预测Q
- 得到loss
-
方法使用
- sample到的一批数据,作为数组直接传进来,(obs,action,reward,next_obs)
-

-
对于获取traget Q
- 按照公式计算
- 对于最后一条数据,通过传入的参数terminal来判断
terminal = layers.cast(terminal, dtype='float32')target = reward + (1.0 - terminal) * self.gamma * best_v- 这两行代码很巧妙的实现了ppt最上面的if。就是最后一步不需要后面的那一块j+1
- 加了一行阻止梯度传播
- 其实就是暂时固定计算target Q的那个网络参数,让他不要时刻更新
-
对于下面这一块获取pred Q value
- 输入obs后,会输出该obs下所有的actions的pred Q value,此时我们只需要某个action的pred Q value
- 这里就是把对应的这个action进行one_hot编码。然后与pred Q value数组按位相乘,再相加,就得到了。
pred_value = self.model.value(obs) # 获取Q预测值
# 将action转onehot向量,比如:3 => [0,0,0,1,0]
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
# 下面一行是逐元素相乘,拿到action对应的 Q(s,a)
# 比如:pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
# ==> pred_action_value = [[3.9]]
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
- 计算loss
pred_action_value与targrt计算均方差,然后扔进优化器
agent.py
核心的算法都在algorithm里面了,但是我们需要feed数据,这些数据就由agent来获取
-
每run一次,就是更新一次
-
build_program方法:这个方法用于构建预测和学习的程序。self.pred_program: 用于动作预测的程序,用来拿到perd的Q值的。self.learn_program: 用于训练(学习)的程序,定义每一个数据的type、shape等。
-
learn方法:这是智能体的学习方法。- 每隔一定步数(由
update_target_steps定义),它会同步模型和目标模型的参数(这是DQN算法中常见的做法)。 - 该方法接收当前状态、动作、奖励、下一个状态和是否为终止状态作为输入,然后执行一次训练步骤。
- 每隔一定步数(由

- sample和predict

总结:举个例子
让我们通过一个简单的强化学习场景来具体说明这个区别。假设我们正在训练一个智能体来玩迷宫游戏,智能体的目标是找到从起点到终点的最短路径。
-
场景设定
-
迷宫游戏:游戏中有墙壁、路径和目标。智能体的任务是找到从起点到终点的路径。
-
智能体(Agent):控制角色在迷宫中移动。
-
算法(Algorithm):决定如何根据当前位置和目标来选择动作。
-
-
Algorithm类中的learn和predict方法- Algorithm类:通常包含强化学习算法的核心逻辑,如Q学习、策略梯度等。它直接与神经网络模型交互,负责计算和更新值函数(例如Q值)或策略。
predict方法:这个方法直接处理模型预测。在迷宫示例中,它可能接收当前位置的状态,并直接使用神经网络模型预测每个可能动作的Q值。learn方法:此方法执行学习过程的核心步骤,比如计算损失函数并更新模型参数。在迷宫示例中,它可能接收一批经历(状态、动作、奖励等)并执行反向传播来改善模型预测。
-
Agent类中的learn和predict方法- Agent类:代表智能体,它是与环境交互的接口。
Agent通常封装了Algorithm,管理与环境的交互、数据预处理、决策和学习过程的细节。
predict方法:在迷宫游戏中,这个方法可能首先对状态进行预处理(比如归一化),然后调用Algorithm的predict方法来获取动作的Q值,并基于这些Q值选择动作(例如使用?-greedy策略)。learn方法:这个方法可能管理学习过程中的一些高层逻辑,如确定何时同步目标网络的参数(在DQN中)。然后它会调用Algorithm的learn方法来实际更新模型。此外,它可能处理与学习相关的其他逻辑,比如更新?值(探索率)。
- Agent类:代表智能体,它是与环境交互的接口。
-
实例解释
-
当智能体在迷宫中探索时,它使用
predict方法来决定下一步动作。predict方法内部调用算法层的predict来评估当前状态下的每个可能动作,然后选择最佳动作。 -
当智能体获得一些经验(例如走了一段路径,得到了一些奖励或惩罚)后,它使用
learn方法来更新其策略。learn方法内部调用算法层的learn来实际进行学习,更新模型以改进智能体在未来做出决策的能力。
-
-
结论
这个例子说明了Agent层如何处理高层逻辑和环境交互(如数据预处理和决定何时学习),而Algorithm层专注于实际的计算和模型更新。这种分层设计有助于代码的组织和复用,同时使智能体的行为和学习过程更加灵活和高效。
实战

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!