被围绕的区域[中等]

一、题目

给你一个m x n的矩阵board，由若干字符X和O，找到所有被X围绕的区域，并将这些区域里所有的O用X填充。

示例 1：

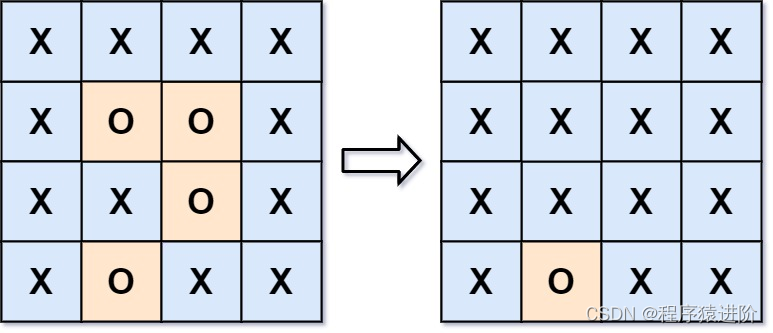
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的O都不会被填充为X。 任何不在边界上，或不与边界上的O相连的O最终都会被填充为X。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：
输入：board = [["X"]]
输出：[["X"]]

::: warning
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j]为X或O
:::

二、代码

本题给定的矩阵中有三种元素：
1、字母X；
2、被字母X包围的字母O；
3、没有被字母X包围的字母O。

本题要求将所有被字母X包围的字母 O都变为字母X，但很难判断哪些O是被包围的，哪些O不是被包围的。

注意到题目解释中提到：任何边界上的O都不会被填充为X。 我们可以想到，所有的不被包围的O都直接或间接与边界上的O相连。我们可以利用这个性质判断O是否在边界上，具体地说：
1、对于每一个边界上的O，我们以它为起点，标记所有与它直接或间接相连的字母O；
2、最后我们遍历这个矩阵，对于每一个字母：如果该字母被标记过，则该字母为没有被字母X包围的字母O，我们将其还原为字母O；如果该字母没有被标记过，则该字母为被字母X包围的字母O，我们将其修改为字母X。

【1】深度优先搜索： 我们可以使用深度优先搜索实现标记操作。在下面的代码中，我们把标记过的字母O修改为字母A。

class Solution {
    int n, m;

    public void solve(char[][] board) {
        n = board.length;
        if (n == 0) {
            return;
        }
        m = board[0].length;
        for (int i = 0; i < n; i++) {
            dfs(board, i, 0);
            dfs(board, i, m - 1);
        }
        for (int i = 1; i < m - 1; i++) {
            dfs(board, 0, i);
            dfs(board, n - 1, i);
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }

    public void dfs(char[][] board, int x, int y) {
        if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
            return;
        }
        board[x][y] = 'A';
        dfs(board, x + 1, y);
        dfs(board, x - 1, y);
        dfs(board, x, y + 1);
        dfs(board, x, y - 1);
    }
}

时间复杂度： O(n×m)，其中n和m分别为矩阵的行数和列数。深度优先搜索过程中，每一个点至多只会被标记一次。
空间复杂度： O(n×m)，其中n和m分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。

【2】广度优先搜索： 我们可以使用广度优先搜索实现标记操作。在下面的代码中，我们把标记过的字母O修改为字母A。

class Solution {
    int[] dx = {1, -1, 0, 0};
    int[] dy = {0, 0, 1, -1};

    public void solve(char[][] board) {
        int n = board.length;
        if (n == 0) {
            return;
        }
        int m = board[0].length;
        Queue<int[]> queue = new LinkedList<int[]>();
        for (int i = 0; i < n; i++) {
            if (board[i][0] == 'O') {
                queue.offer(new int[]{i, 0});
                board[i][0] = 'A';
            }
            if (board[i][m - 1] == 'O') {
                queue.offer(new int[]{i, m - 1});
                board[i][m - 1] = 'A';
            }
        }
        for (int i = 1; i < m - 1; i++) {
            if (board[0][i] == 'O') {
                queue.offer(new int[]{0, i});
                board[0][i] = 'A';
            }
            if (board[n - 1][i] == 'O') {
                queue.offer(new int[]{n - 1, i});
                board[n - 1][i] = 'A';
            }
        }
        while (!queue.isEmpty()) {
            int[] cell = queue.poll();
            int x = cell[0], y = cell[1];
            for (int i = 0; i < 4; i++) {
                int mx = x + dx[i], my = y + dy[i];
                if (mx < 0 || my < 0 || mx >= n || my >= m || board[mx][my] != 'O') {
                    continue;
                }
                queue.offer(new int[]{mx, my});
                board[mx][my] = 'A';
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }
}

时间复杂度： O(n×m)，其中n和m分别为矩阵的行数和列数。广度优先搜索过程中，每一个点至多只会被标记一次。
空间复杂度： O(n×m)，其中n和m分别为矩阵的行数和列数。主要为广度优先搜索的队列的开销。