CGAL的锥形扳手

1、介绍

????????这一章描述了用于构建两种基于锥体的生成树的包：Yao图和Theta图，给定平面上的一组顶点和锥体边界的方向。支持精确和不精确的构造。在精确构造中，锥体边界是使用多项式的根来计算的，通过避免在计算中使用π来实现精确性。在不精确构造中，锥体边界是用π值的浮点近似来计算的，对于大多数应用来说仍然足够准确。此外，为了可视化目的，本章描述了一个全局函数，它可以将构造好的图作为输入，生成用于Gnuplot绘制该图的数据和脚本文件。

????????Yao图和Theta图：这是两种基于锥体的生成树，用于在平面上的点集之间构建图形。这些图形在计算几何和图形学中有广泛应用。

????????精确和不精确构造：精确构造使用数学上的精确方法来计算锥体的边界，而不精确构造使用近似值。精确构造通常更准确，但可能计算成本更高。

2、定义

????????这一部分详细定义了Yao图和Theta图，这些定义在我们的实现中得到了遵循。特别是，因为这个包支持精确构建Yao图和Theta图，我们需要明确锥体边界属于哪个锥体。这里提出的定义对此进行了澄清。

????????给定平面上的一组顶点V，整数参数k（k>1）的有向Yao图可按照以下方式获得。对于每个顶点u∈V，从给定的方向（例如，正x轴的方向）开始，从u逆时针绘制k条等距射线l0、l1、...、lk-1（见下图）。这些射线将平面划分为k个角度为2π/k的锥体，分别按逆时针顺序标记为c(u,0)、c(u,1)、...、c(u,k-1)。为避免在边界处重叠，这里规定c(u,i)的区域，其中i=0，…，k-1，包含射线li但不包含射线l(i+1)%k。

????????在u的每个锥体中，通过该锥体中的欧几里得距离从u绘制到其最近顶点的有向边。任意打破平衡。这些有向边将形成V上有向Yao图的边集。V上的无向Yao图是通过忽略边的方向获得的。请注意，如果边uv和vu都在有向Yao图中，则无向Yao图中只存在一条边uv。下图（b）给出了k=5时Yao图的一个示例。

????????锥体和k=5的Yao图示例。?

????????类似于 Yao 图，有向或无向的 Theta 图也是通过让每个顶点 u∈V 在它的每个锥体中选择一个最接近的顶点来形成边而得到的。唯一的区别是，Theta 图中的最接近意味着在该锥体的平分线上投影距离最小，而不是直接欧几里得距离。例如，在图中，顶点 u 的最接近的顶点将是顶点 b。

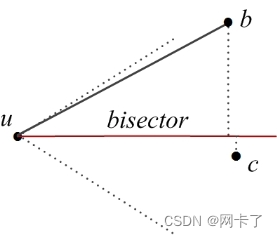
?Theta图的圆锥中的平分线。

????????Yao图和Theta图的变体是Half Yao图和Half Theta图。 不同之处在于只绘制偶数或奇数锥体中的边。 例如，在k=6的Theta图的偶数情况下，只绘制锥体c(u,0)、c(u,2)和c(u,4)中的边。

3、软件设计

????????此包提供了以下模板函子：

????????Compute_cone_boundaries_2：给定锥体编号和初始方向，用于计算锥体边界方向的函子。

????????Construct_theta_graph_2：给定平面上一组顶点，用于构造Theta图的函子。

????????construct_yao_graph_2：给定平面上一组顶点，构造 Yao 图用的函子。

????????除了这些函子，为了可视化构造的图形，该软件包提供了一个名为CGAL::gnuplot_output_2()的全局函数，用于将boost::adjacency_list数据结构输出到Gnuplot数据和脚本文件。下面，我们详细介绍上述函子和函数的设计和使用。

3.1、计算圆锥体边界

????????函子 Compute_cone_boundaries_2 具有以下定义。

template <typename Traits>
class Compute_cone_boundaries_2;

?????????模板参数 Traits 决定了锥体边界的计算是精确的还是不精确的。如果此参数是 Exact_predicates_exact_constructions_kernel_with_root_of，则计算将是精确的；如果此参数是 Exact_predicates_inexact_constructions_kernel，则计算将是不精确的。

????????精确计算是基于这样一个事实，即当锥角 θ 是 2π/n 的形式，其中 n 是一个正整数时，sin(θ) 和 cos(θ) 可以通过多项式的根精确表示，从而避免在计算中使用 π。精确计算要求数字类型为 CORE::Expr 或 leda_real。在不精确计算中，锥角 θ 简单地计算为 2π/k，其中 k 是锥体的数量，π 取常数 CGAL_PI=3.14159265358979323846 的值。然后，计算 sin(θ) 和 cos(θ)。虽然不精确计算是通过一般的函子定义完成的，但精确计算是通过这个函子的一个特化来完成的。

????????该函子目前被用于构造Theta和Yao图的函子Construct_theta_graph_2和Construct_yao_graph_2。该函子还可以用于其他需要将平面划分为等角锥体的应用。关于如何在编写应用程序时使用此函子来计算锥体边界，请参阅“示例”部分。

3.2、构造Theta图

????????函子Construct_theta_graph_2具有以下定义

template <typename Traits, typename Graph>
class Construct_theta_graph_2;

????????与函子 Compute_cone_boundaries_2 类似，模板参数 Traits 决定了 Theta 图是精确构建还是非精确构建。模板参数 Graph 指定了用于存储所构建图的图类型。我们的软件包要求它来自 Boost Graph Library (BGL) 的 boost::adjacency_list。

????????使用 boost::adjacency_list 的优点是它为所构建图的进一步处理提供了便利，因为 BGL 包含最常见的图算法。请注意，BGL 共提供了两个模板类来表示图：boost::adjacency_list 和 boost::adjacency_matrix，前者适用于稀疏图，后者适用于稠密图。

????????虽然基于锥体的扳手是稀疏图，并且 boost::adjacency_list 和 boost::adjacency_matrix 提供的接口是不同的，但我们的软件包只支持 boost::adjacency_list。

????????请注意，BGL中的boost::adjacency_list有七个模板参数：OutEdgeList、VertexList、Directed、VertexProperties、EdgeProperties、GraphProperties、EdgeList，其中我们需要VertexProperties为 Traits::Point_2，其他参数可以自由选择。另请注意，在这里我们将Point_2直接作为捆绑属性传递给boost：：adjacency_list，因为这使得我们的实现比使用属性映射更简单。如果你想要除Point_2之外的更多属性，你仍然可以使用属性映射构造外部属性。

????????在构建Theta图时，该函子使用了Narasimhan和Smid提出的算法。基本上，它是一种扫线算法，并使用平衡搜索树来存储已经扫描过的顶点。它的复杂度为O(nlogn)，其中n是平面中的顶点数量。这一复杂度已被证明是最优的。

????????有关如何使用此 Construct_theta_graph_2 函子编写构建 Theta 图的应用程序的更多详细信息。

3.3、构建一个 Yao 图

????????函子Construct_yao_graph_2具有与Construct_theta_graph_2类似的定义。

template <typename Traits, typename Graph>
class Construct_yao_graph_2;

????????这两个模板参数的使用方法与 Construct_theta_graph_2 相同，因此请参阅上一小节的详细信息。我们在这里注意到，Yao 图的构造算法是对构造 Theta 图算法的轻微改编，复杂度为 O(n2)。这种改编增加了复杂度，因为在构造 Theta 图时，可以通过平衡搜索树来搜索投影距离“最近”的节点，但在构造 Yao 图时，通过欧几里德距离搜索“最近”的节点无法通过平衡搜索树来完成。

????????请注意，在[1]中描述了一种复杂度为O(nlogn)的构建Yao图的最优算法。但是，与当前实现的算法相比，该算法的实现要复杂得多，并且它几乎不能重用构建Theta图的代码，因此目前没有在该包中实现。

3.4、Gnuplot输出

????????这个包还实现了一个模板函数CGAL::gnuplot_output_2（），它读取一个boost::adjacency_list?对象，并生成两个文件，供gnuplot用来可视化存储在boost:adjacency_list?对象中的图形。此模板函数具有以下定义：

template <typename Graph_>
void gnuplot_output_2(const Graph_& g, const std::string& prefix);

?????????模板参数 Graph_ 指定要绘制的图形的类型。要使此函数工作，图形类型必须是 boost::adjacency_list，Point_2 作为 VertexProperties。至于函数的两个参数，g 给出要绘制的图形，prefix 给出函数生成的文件的名称前缀。具体来说，此函数将生成以下两个文件：

????????一个名为prefix.v的数据文件，其中包含每个顶点的（x，y）坐标。为了使Gnuplot能够读取，无论在CGAL内核中使用哪种数字类型，（x，y）坐标都以十进制格式写入数据文件。这是通过在输出x或y坐标之前调用to_double（）来实现的。

????????一个名为prefix.plt的Gnuplot脚本文件，由Gnuplot加载以绘制顶点集和边集。顶点集从上述数据文件中读取，边集包含在脚本文件中，语法为set arrow from x1, y1 to x2, y2。

4、其他

????????Theta图（Theta Graph）和Yao图（Yao Graph）是两种在几何图论中常用的稀疏跨度图（Sparse Spanner Graph）。这些图被设计用于在保持图中所有顶点对之间的最短路径长度的同时，减少图的边数。这在路由、网络设计和无线传感器网络等领域非常有用。

????????Theta图（Theta Graph）：Theta图是一种基于锥体（Cone）的稀疏跨度图。对于平面上的每个点，它考虑该点周围的所有方向，并将这些方向划分为等宽的锥体。如果两个点位于彼此的锥体内，并且它们之间没有更近的第三个点，则在这两点之间画一条边。Theta图保留了原始点集中所有点对之间的最短路径，同时具有较少的边数，这使其在计算上更加高效。

????????Yao图（Yao Graph）：Yao图也是一种稀疏跨度图，但它采用了不同的方法来确定边的存在。对于平面上的每个点，它考虑该点的所有邻居，并为每个邻居分配一个锥体。然后，对于每个锥体，它选择最近的邻居并在这两点之间画一条边。Yao图的一个关键特性是，对于每个点，它的边数最多与锥体的数量成比例，这导致图的边数总体上较少。Yao图也保留了原始点集中所有点对之间的最短路径。

????????这两种图在理论和实践中都很有用，因为它们提供了在保持关键距离信息的同时降低图形复杂性的方法。这对于需要快速和高效路径规划的应用来说特别重要，如机器人导航、通信网络和其他需要地理空间理解的场景。

????????boost::adjacency_list?是 Boost Graph Library (BGL) 中的一个核心类，用于表示图数据结构。Boost Graph Library 是一个泛型图库，旨在为各种图算法提供一个统一和高效的接口。boost::adjacency_list?提供了一种灵活的方式来表示有向图、无向图、多重图等。

????????基本概念在使用?boost::adjacency_list?之前，了解以下几个基本概念是有帮助的：

????????顶点 (Vertex): 图中的一个点。

????????边 (Edge): 连接两个顶点的线。

????????有向图与无向图: 在有向图中，边有方向；在无向图中，边没有方向。

????????多重图: 允许有重复的边和自环的图????????

#include <boost/graph/adjacency_list.hpp>  
using namespace boost;  
  
typedef adjacency_list<vecS, vecS, undirectedS> Graph;