NNDL总结
第四章 前馈神经网络
4.1 神经元
?人工神经元,简称神经元,是构成神经网络的基本单元。
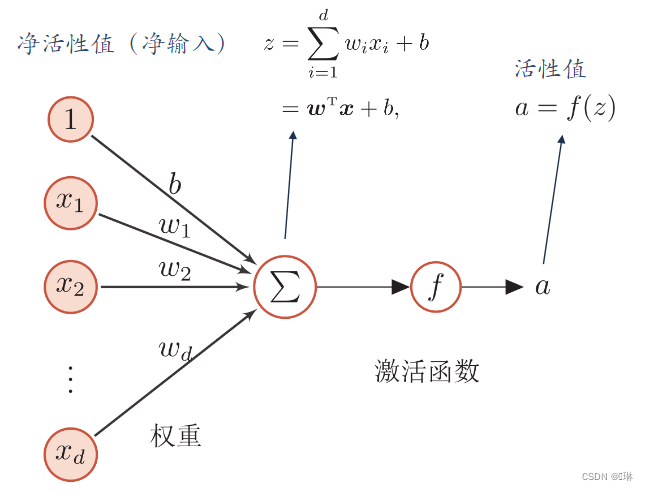
?当>0时,
为1,兴奋;?当
<0时,
为0,抑制。
激活函数的性质
1、连续可导的非线性函数。
2、激活函数及其导函数要尽可能简单
3、激活函数的导函数的值域要在一个合适的区间内
4、单调递增(不一定)
常用的激活函数
S型函数
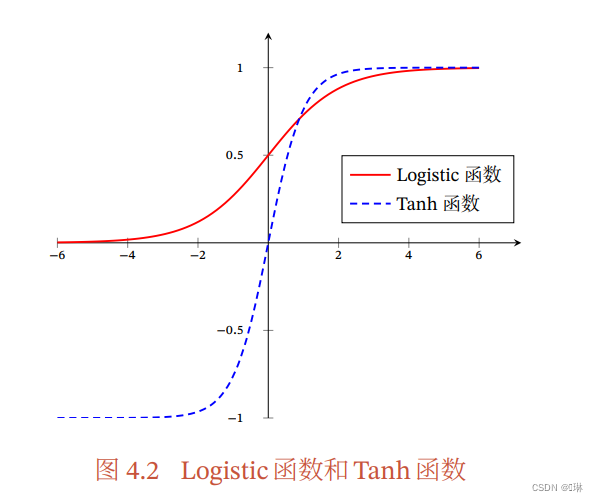
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Logistic函数:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Tanh函数:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
性质:
饱和函数
Tanh函数是零中心化,而logistic函数的输出恒大于0? ? ?
(非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移,并进一步使得梯度下降的收敛速度变慢)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
斜坡函数?

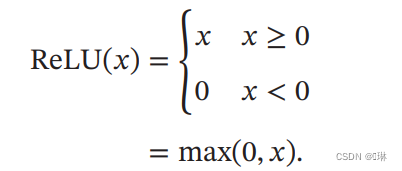
ReLU可以解决梯度消失问题?
死亡ReLU问题(Dying ReLU Problem)
训练时,如果参数在一次不恰当的更新后(如:学习率过大), 第一个隐藏层中某个 ReLU神经元在所有训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活。

4.2 网络结构
目前常用的神经网络结构有以下三种:
前馈网络
前馈网络包括全连接前馈网络和卷积神经网络。
前馈网络可以看作一个函数,通过简单非线性函数的多次复合,实现输入空间到输出空间的复杂映射。这种网络结构简单,易于实现。
记忆网络
记忆网络,也称反馈网络,网络中的神经元不但可以接受其他神经元的信息,也可以接受自己的历史信息。具有记忆能力。
图网络
图网络是前馈网络和记忆网络的泛化,包含很多不同的实现方式,比如图卷积网络、图注意力网络、消息传递神经网络等。?

4.3 前馈神经网络
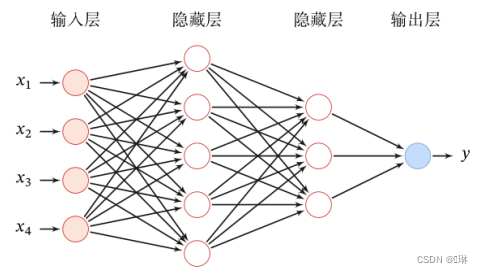
前馈神经网络(全连接神经网络、多层感知器)
? ? 各神经元分别属于不同的层,层内无连接。
? ? 相邻两层之间的神经元全部两两连接(全连接)。
? ? 整个网络中无反馈,信号从输入层向输出层单向传播。
? ? 可用一个有向无环图表示。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
可合并写为:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
首先根据第?1层神经元的活性值
计算出第
层神经元的净活性值
,然后经过一个激活函数得到第
层神经元的活性值。因此,我们也可以把每个神经层看作一个仿射变换和一个非线性变换。?
参数学习
 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
权重衰减:抑制过拟合
对于所有权重,权值衰减方法都会为损失函数加上
。因此,在求权重梯度的计算中,要为之前的误差反向传播的结果加上正则化的导数
。
?、
范数见:梯度爆炸实验-CSDN博客
4.4 反向传播算法
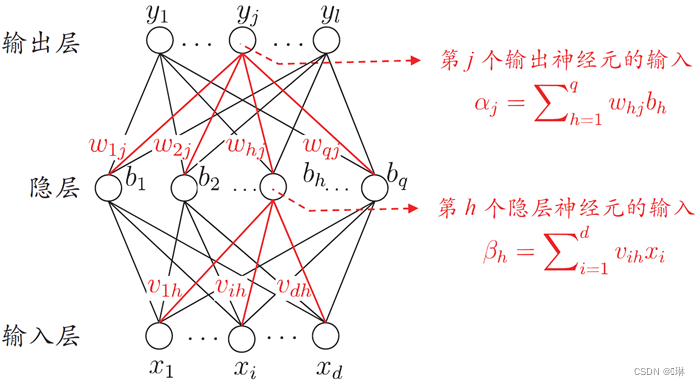
?前向计算
step1:? ? ? ? ? ? ? ? ? ??
step2:? ? ? ? ? ? ? ? ? ?
step3:? ? ? ? ? ? ? ? ??
?下面是反向传播的过程推导,当时手推的时候真的很麻烦,很费人。(ο??????????ο?????????)
作业4:实现例题中的前馈神经网络_前馈神经网络计算例题-CSDN博客

4.5?优化算法
非凸优化问题因为可行域集合可能存在无数个局部最优点,通常求解全局最优的算法复杂度是指数级别的(NP难)。
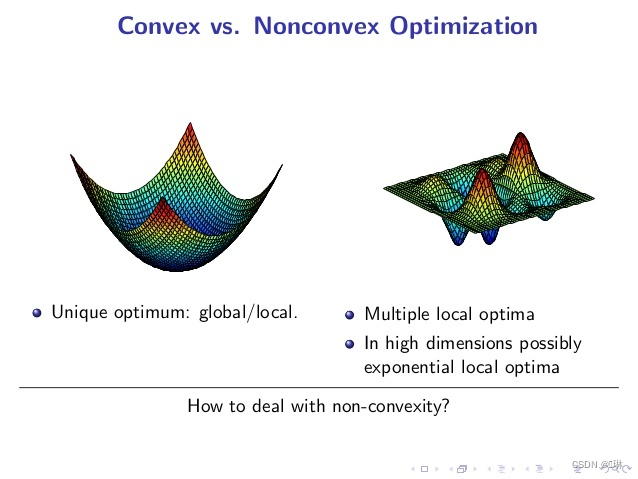
?平方误差损失和交叉熵损失都是关于参数的非凸函数。
梯度消失?

?Sigmoid型函数的饱和区的导数更接近于0,误差经过每一层传递都会不断衰减。当网络层数很深时,梯度就会不停衰减,甚至消失,这就是梯度消失问题。
?第五章 卷积神经网络
卷积神经网络是一种具有局部连接、权重共享等特性的深层前馈神经网络.?
全连接神经网络缺点:
1. 参数过多,效率低下,训练困难;会导致过拟合。
2. 将图像展开为向量,会丢失空间信息。
3. 局部不变性特征:自然图像中的物体都具有局部不变性特征。全连接前馈网络很难提取这些局部不变特征。一般需要进行数据增强来提高性能。
目前的卷积神经网络一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络。卷积神经网络有三个结构上的特性:局部连接、权重共享以及汇聚。
5.1 卷积
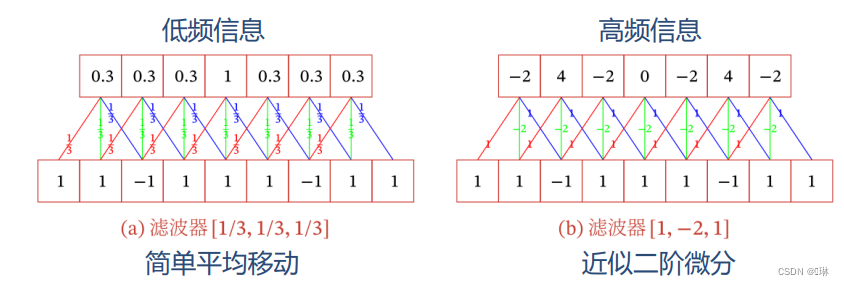
?一维卷积经常用在信号处理中,用于计算信号的延迟累积。不同滤波器(卷积核)提取信号序列中的不同特征。
?二维卷积
?一个输入信息和滤波器
的二维卷积定义为:? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???

?
?互相关和卷积的区别仅仅在于卷积核是否进行翻转。互相关也可以称为不翻转卷积。
?卷积的变种
?引入卷积核的滑动步长和零填充来增加卷积的多样性,可以更灵活地进行特征抽取。
?步长(Stride)是指卷积核在滑动时的时间间隔。
零填充(Zero Padding)是在输入向量两端进行补零?。
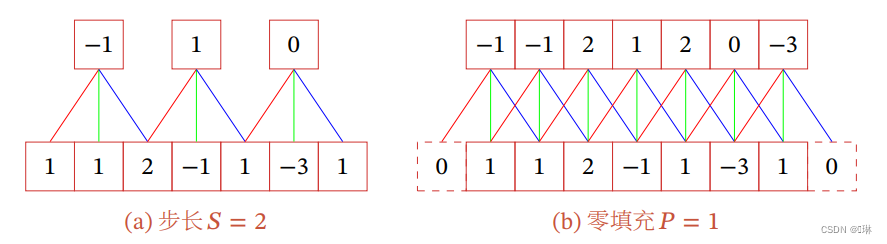
假设卷积层的输入神经元个数为,卷积大小为
,步长为
,在输入两端各 填补
个0(zero padding),那么该卷积层的神经元数量为
一般常用的卷积有以下三类:
(1) 窄卷积(Narrow Convolution):步长 ,两端不补零
,卷积 后输出长度为
。
(2) 宽卷积(Wide Convolution):步长,两端补零
,卷积 后输出长度
。
(3) 等宽卷积(Equal-Width Convolution):步长 ,两端补零
,卷积后输出长度
。
?感受野:特征图上一个点对应输入图像上的区域

5.2?卷积神经网络
?根据卷积的定义,卷积层有两个很重要的性质:局部连接和权重共享。
局部连接:每个神经元没有必要对全局图像进行感知, 只需要对局部进行感知, 然后在更高层将局部的信息综合起来就得到了全局的信息。
权值共享:减少了参数量
?特征映射(Feature Map)为一幅图像(或其他特征映射)在经过卷积提取到的特征,每个特征映射可以作为一类抽取的图像特征。
卷积层可显著减少连接个数,但每一个特征映射的神经元个数并没显著减少。
汇聚层可有效地减少神经元的数量。
汇聚层(Pooling Layer)也叫子采样层(Subsampling Layer),其作用是进行特征选择,降低特征数量,从而减少参数数量。
常用的汇聚函数有两种:
(1)最大汇聚:对于一个区域
,选择这个区域内所有神经元的最大活性值作为这个区域的表示。
(2)平均汇聚:一般是取区域内所有神经元活性值的平 均值。
?卷积网络的整体结构
卷积层、汇聚层、全连接层交叉堆叠而成。

5.3 参数学习
卷积的性质
?交换性:图像
和 卷积核
有固定长度时,它们的宽卷积具有交换性
导数:
?CNN的反向传播算法:https://www.cnblogs.com/pinard/p/6494810.html
5.4 几种典型的卷积神经网络
?LeNet-5

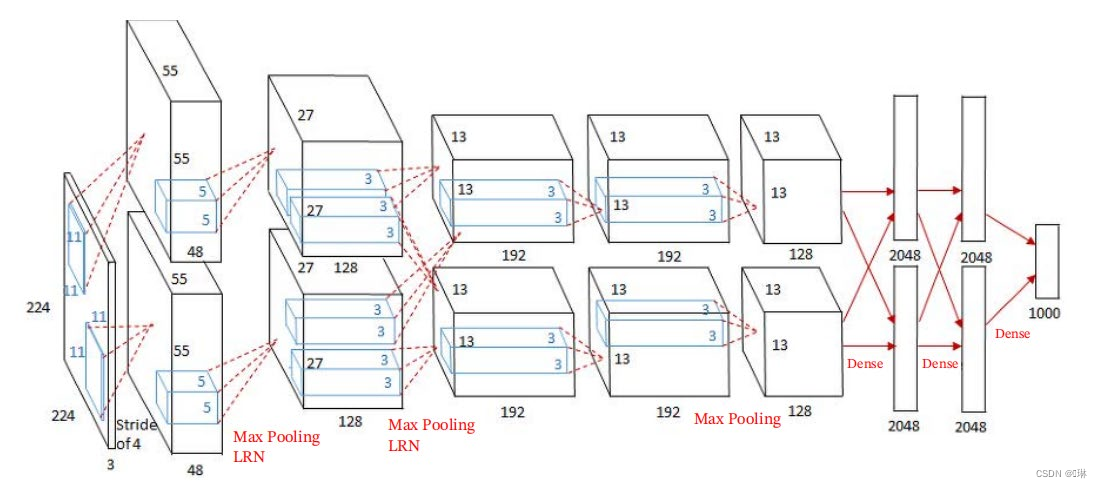
?AlexNet(2012第一个现代深度卷积网络模型)
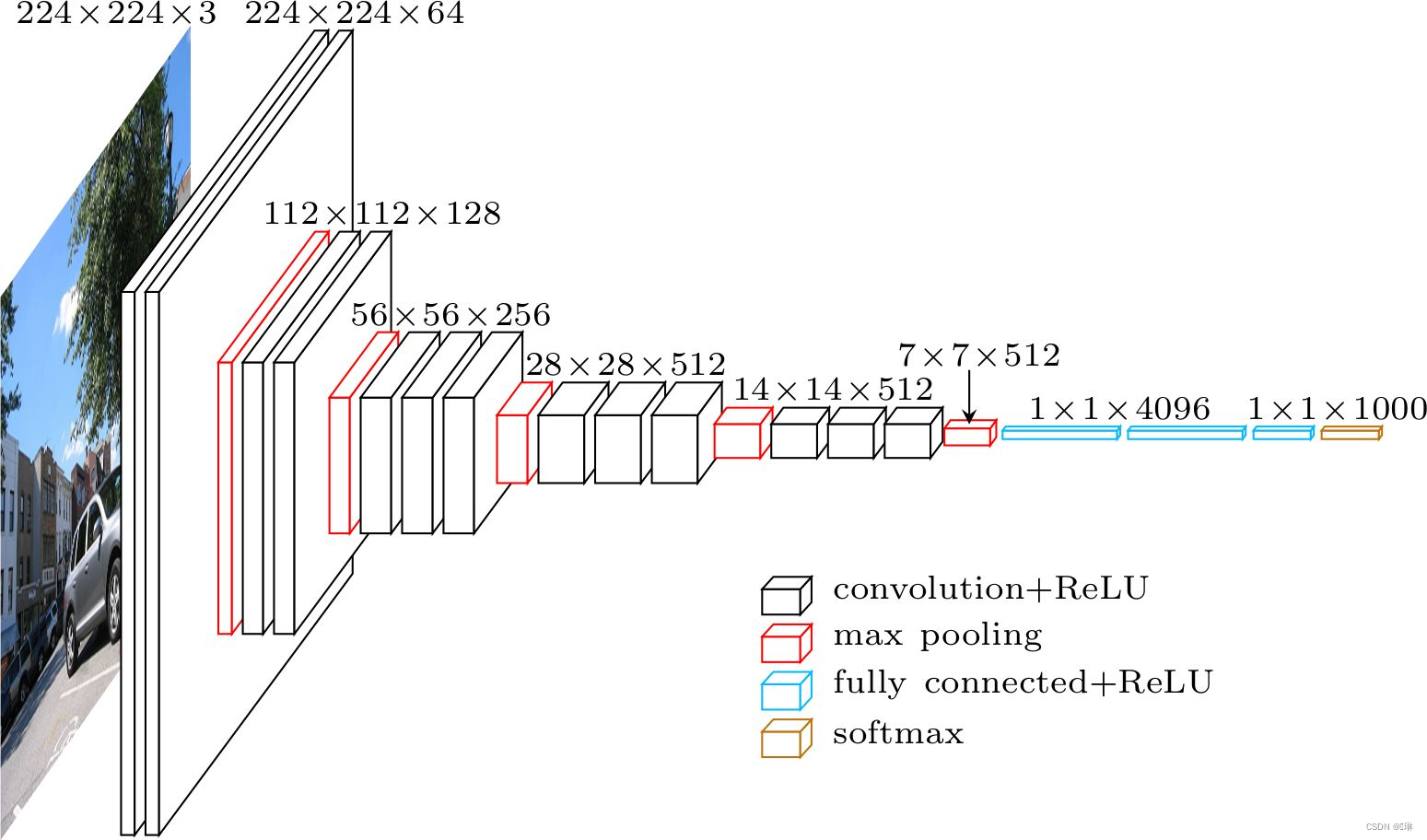
?VGG-Net
更小的卷积核
卷积核不超过3×3
2个3×3卷积核堆叠的感受野相当于 1个5×5卷积核
同等感受野,2个3×3卷积间加入激活函数,其非线性能力比1个5×5卷积强
更深的网络结构
AlexNet:5个卷积层
VGG16:13个卷积层
更深的结构有助于网络提取图像中更复杂的语义信息
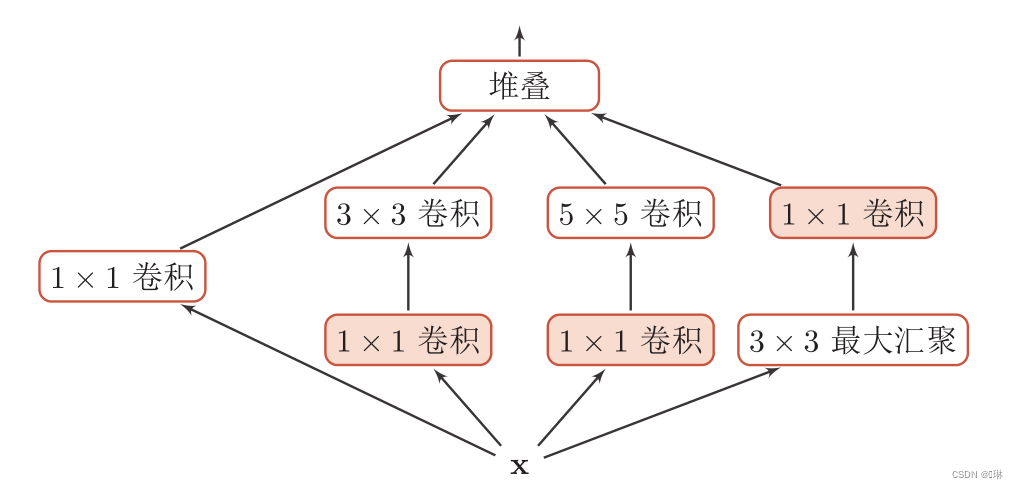
 ?Inception网络
?Inception网络
?Inception模块:一个卷积层包含多个不同大小的卷积操作
残差网络通过给非线性的卷积层增加直连边(也称为残差连接(Residual Connection))的方式来提高信息的传播效率。

?残差网络就是将很多个残差单元串联起来构成的一个非常深的网络。
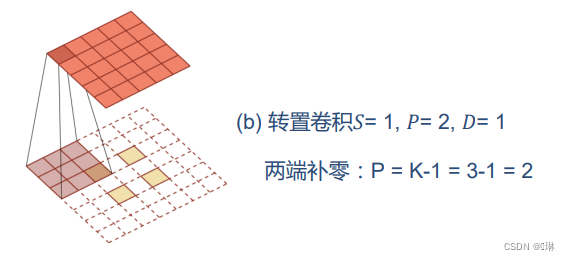
5.5 其他卷积方式
转置卷积
微步卷积:步长
的转置卷积
输入特征之间插入0,间接使得步长变小?
如果卷积操作的步长为
,希望其对应的转置卷积的步长为
, 需要在输入特征之间插入
个0来使得其移动的速度变慢.
空洞卷积
在卷积核的每两个元素之间插入D ? 1个空洞, 卷积核的有效大小为:
第六章 循环神经网络

前馈网络存在的问题
连接在层与层之间,每层节点间无连接。 输入和输出的维数固定,不能任意改变。无法处理时序数据。
循环神经网络(Recurrent Neural Network,RNN)
? ? ? 1、具有短期记忆能力
? ? ? 2、神经元可接受其他神经元信息,也可接受自身信息,形成有 环路的网络结构
? ? ? 3、和前馈神经网络相比,更加符合生物神经网络的结构
? ? ? 4、已广泛应用在语音识别、语言模型、自然语言生成等任务上
? ? ? 5、容易扩展到更广义的记忆网络模型:递归神经网络、图网络
6.1 给网络增加记忆力
三种方法增加短期记忆能力:
延时神经网络
? ? 建立额外延时单元,存储网络历史信息
有外部输入的非线性自回归模型
? ? 用变量
的历史信息来预测自己
循环神经网络
? ? RNN通过使用带自反馈的神经元,能够处理任意长度的时序数据。
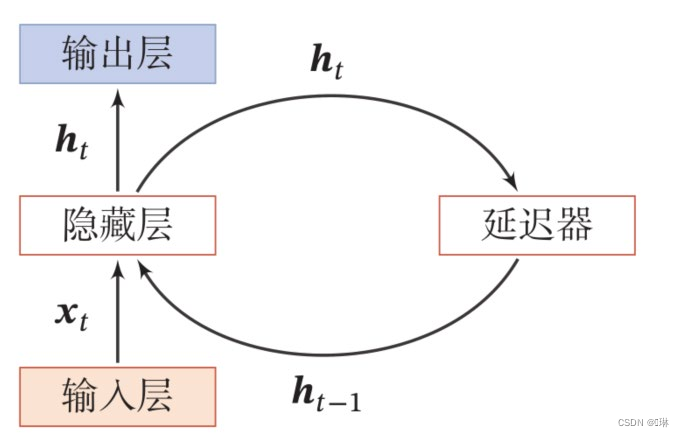
6.2 简单循环网络
?SRN:只有一个隐藏层的神经网络
6.3 应用到机器学习
序列到类别:主要用于序列数据的分类问题:输入为序列,输出为类别。
同步的序列到序列:主要用于序列标注任务,即每一时刻都有输入和输出,输入序列和输出序列的长度相同。
异步的序列到序列:也称为编码器—解码器模型,即输入序列和输出序列不需要有严格的对应关系,也不需要保持相同的长度。
6.4 参数学习
在循环神经网络中主要有两种计算梯度的方式:随时间反向传播算法(BPTT)和实时循环学习算法(RTRL)?。? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ??
?随时间反向传播算法的主要思想是通过类似前馈神经网络的误差反向传播算法来计算梯度。
?实时循环学习是通过前向传播的方式来计算梯度

6.5 长程依赖问题
?循环神经网络在学习过程中的主要问题是由于梯度消失或爆炸问题,很难建模长时间间隔的状态之间的依赖关系。
梯度爆炸 一般而言,循环网络的梯度爆炸问题比较容易解决,一般通过权重衰减或梯度截断来避免。
梯度消失 梯度消失是循环网络的主要问题.除了使用一些优化技巧外,更有效的方式就是改变模型。通过引入门控机制来进一步改进模型。
6.6 基于门控的循环神经网络
基于门控的循环神经网络:长短期记忆网络和门控循环单元网络。
长短期记忆网络(LSTM)是循环神经网络的一个变体,可以有效地解决简单循环神经网络的梯度爆炸或消失问题.

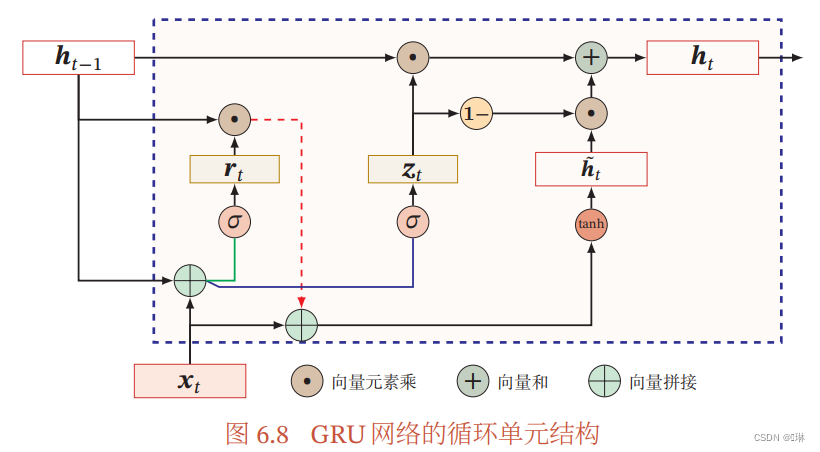
门控循环单元(GRU)网络是一种比LSTM网络更加简单的循环神经网络。
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!